Page 267 - Geochemical Anomaly and Mineral Prospectivity Mapping in GIS

270 Chapter 8

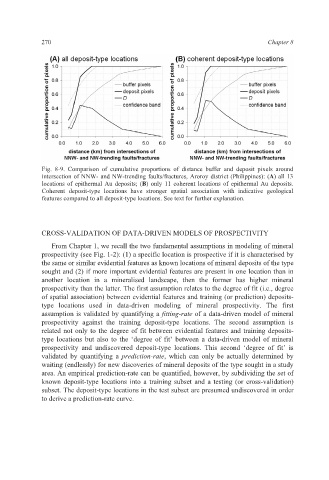
Fig. 8-9. Comparison of cumulative proportions of distance buffer and deposit pixels around
intersection of NNW- and NW-trending faults/fractures, Aroroy district (Philippines): (A) all 13
locations of epithermal Au deposits; (B) only 11 coherent locations of epithermal Au deposits.
Coherent deposit-type locations have stronger spatial association with indicative geological
features compared to all deposit-type locations. See text for further explanation.

CROSS-VALIDATION OF DATA-DRIVEN MODELS OF PROSPECTIVITY

From Chapter 1, we recall the two fundamental assumptions in modeling of mineral
prospectivity (see Fig. 1-2): (1) a specific location is prospective if it is characterised by
the same or similar evidential features as known locations of mineral deposits of the type
sought and (2) if more important evidential features are present in one location than in
another location in a mineralised landscape, then the former has higher mineral
prospectivity than the latter. The first assumption relates to the degree of fit (i.e., degree
of spatial association) between evidential features and training (or prediction) deposits-
type locations used in data-driven modeling of mineral prospectivity. The first
assumption is validated by quantifying a fitting-rate of a data-driven model of mineral
prospectivity against the training deposit-type locations. The second assumption is
related not only to the degree of fit between evidential features and training deposits-
type locations but also to the ‘degree of fit’ between a data-driven model of mineral
prospectivity and undiscovered deposit-type locations. This second ‘degree of fit’ is
validated by quantifying a prediction-rate, which can only be actually determined by
waiting (endlessly) for new discoveries of mineral deposits of the type sought in a study
area. An empirical prediction-rate can be quantified, however, by subdividing the set of
known deposit-type locations into a training subset and a testing (or cross-validation)
subset. The deposit-type locations in the test subset are presumed undiscovered in order
to derive a prediction-rate curve.