Page 135 - Geometric Modeling and Algebraic Geometry

136 T. Beck and J. Schicho
For example ν 1 and its conjugate with respect to the Galois extension Q(γ 1 ) | Q
correspond to two points in the preimage π −1 (Q 1 ). We compute the adjoint orders
for these valuations (and their conjugates):

d ϕ 1 (u 1 )
d f 1
− ord t
d t
=ord t ϕ 1
α ν 1
d v 1
=ord t (( 129 + 128γ 1 )t +(− 3225 − 3200 γ 1 )t + ... ) − ord t (1)
3
2
4 76 19
=2 − 0=2

d ϕ 2 (u 1 )
d f 1
− ord t
d t
=ord t ϕ 2
α ν 2
d v 1
=ord t ((6 + 8γ 2 )t +( 39 +26γ 2 )t + ... ) − ord t (1)
3
2
2
=2 − 0=2
7.7.2 Checking rationality
The number of interior points of Π(f) is equal to 4. Again from [8, p. 1620], we see
=2. Hence genus(C)=4 − 2 − 2=0 and C is parametrizable.
that δ Q 1
= δ Q 2
7.7.3 Computing two adjoints
s s s

r r r
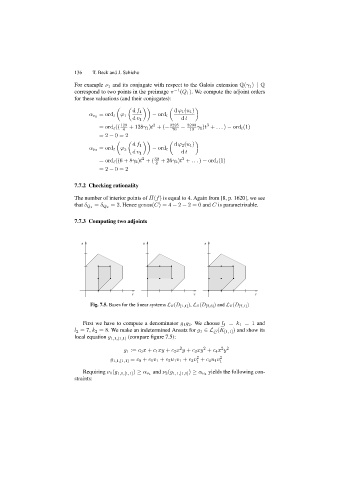
Fig. 7.5. Bases for the linear systems L S(D [1,1] ), L S(D [7,8] ) and L S(D [7,1] )

First we have to compute a denominator g 1 g 2 . We choose l 1 = k 1 =1 and
(K [1,1] ) and show its

l 2 =7, k 2 =8. We make an indetermined Ansatz for g 1 ∈L C
local equation g 1,1,[1,1] (compare figure 7.5):
g 1 := c 0 x + c 1 xy + c 2 x y + c 3 xy + c 4 x y
2
2
2 2
g 1,1,[1,1] = c 0 + c 1 v 1 + c 2 u 1 v 1 + c 3 v + c 4 u 1 v 2
2
1 1
yields the following con-
and ν 2 (g 1,1,[1,1] ) ≥ α ν 2
Requiring ν 1 (g 1,1,[1,1] ) ≥ α ν 1
straints: