Page 163 - Geometric Modeling and Algebraic Geometry

9 Intersecting Biquadratic Patches 165
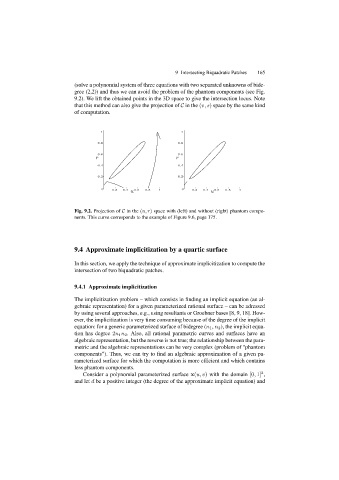
(solve a polynomial system of three equations with two separated unknowns of bide-
gree (2,2)) and thus we can avoid the problem of the phantom components (see Fig.
9.2). We lift the obtained points in the 3D space to give the intersection locus. Note
that this method can also give the projection of C in the (v, s) space by the same kind
of computation.

1 1

0.8 0.8
0.6 0.6
r r
0.4 0.4

0.2 0.2

0 1 0 1
0.2 0.4 u 0.6 0.8 0.2 0.4 u 0.6 0.8

Fig. 9.2. Projection of C in the (u, r) space with (left) and without (right) phantom compo-
nents. This curve corresponds to the example of Figure 9.6, page 175.

9.4 Approximate implicitization by a quartic surface

In this section, we apply the technique of approximate implicitization to compute the
intersection of two biquadratic patches.

9.4.1 Approximate implicitization

The implicitization problem – which consists in finding an implicit equation (an al-
gebraic representation) for a given parameterized rational surface – can be adressed
by using several approaches, e.g., using resultants or Groebner bases [8, 9, 18]. How-
ever, the implicitization is very time consuming because of the degree of the implicit
equation: for a generic parameterized surface of bidegree (n 1 , n 2 ), the implicit equa-
tion has degree 2n 1 n 2 . Also, all rational parametric curves and surfaces have an
algebraic representation, but the reverse is not true; the relationship between the para-
metric and the algebraic representations can be very complex (problem of “phantom
components”). Thus, we can try to find an algebraic approximation of a given pa-
rameterized surface for which the computation is more efficient and which contains
less phantom components.
Consider a polynomial parameterized surface x(u, v) with the domain [0, 1] ,
2
and let d be a positive integer (the degree of the approximate implicit equation) and