Page 90 - Geothermal Energy Renewable Energy and The Environment

Chemistry of Geothermal Fluids 75

2.0
Halite
1.0 + –
Na + Cl
0.0

Log K –1.0 Geothermal waters

–2.0
Quartz
–3.0 SiO (aq)
2
–4.0

–5.0
0 50 100 150 200 250 300 350
T (°C)
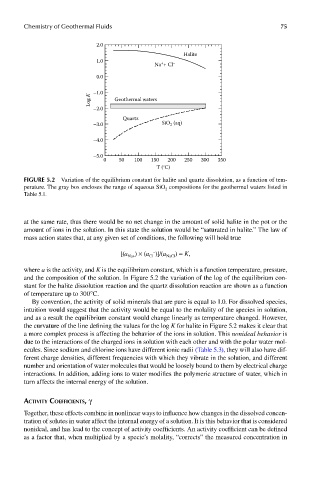
FIGUre 5.2 Variation of the equilibrium constant for halite and quartz dissolution, as a function of tem-
perature. The gray box encloses the range of aqueous SiO 2 compositions for the geothermal waters listed in
Table 5.1.

at the same rate, thus there would be no net change in the amount of solid halite in the pot or the
amount of ions in the solution. In this state the solution would be “saturated in halite.” The law of
mass action states that, at any given set of conditions, the following will hold true

–
[(a Na+ ) × (a )]/(a NaCl ) = K,
Cl
where a is the activity, and K is the equilibrium constant, which is a function temperature, pressure,
and the composition of the solution. In Figure 5.2 the variation of the log of the equilibrium con-
stant for the halite dissolution reaction and the quartz dissolution reaction are shown as a function
of temperature up to 300°C.
By convention, the activity of solid minerals that are pure is equal to 1.0. For dissolved species,
intuition would suggest that the activity would be equal to the molality of the species in solution,
and as a result the equilibrium constant would change linearly as temperature changed. However,
the curvature of the line defining the values for the log K for halite in Figure 5.2 makes it clear that
a more complex process is affecting the behavior of the ions in solution. This nonideal behavior is
due to the interactions of the charged ions in solution with each other and with the polar water mol-
ecules. Since sodium and chlorine ions have different ionic radii (Table 5.3), they will also have dif-
ferent charge densities, different frequencies with which they vibrate in the solution, and different
number and orientation of water molecules that would be loosely bound to them by electrical charge
interactions. In addition, adding ions to water modifies the polymeric structure of water, which in
turn affects the internal energy of the solution.

acTiviTy coefficienTs, γ

Together, these effects combine in nonlinear ways to influence how changes in the dissolved concen-
tration of solutes in water affect the internal energy of a solution. It is this behavior that is considered
nonideal, and has lead to the concept of activity coefficients. An activity coefficient can be defined
as a factor that, when multiplied by a specie’s molality, “corrects” the measured concentration in