Page 246 - Glucose Monitoring Devices

250 CHAPTER 12 Modeling the CGM measurement error

(ii) Sensor lag: the time of glucose transport from the interstitium to the sensor
needle in Eq. (12.6). Considering that these are two sequential first-order
diffusion models, we modeled them with one diffusion equation where the
time lag is the resultant single diffusion process representing both the physi-
ological lag and the sensor lag. Empirical estimation gives a time lag of 5 min
(which produces a delay of approximately 15 min).
(iii) The noise of the sensor is nonwhite, non-Gaussian. We, therefore, used an
ARMA process for its modeling. Based on the analysis of the empirical partial
autocorrelation function in dataset 2, we restricted this model to a simple
autoregressive model of order 1 (see Eq. 12.7):

e 1 ¼ v 1 e n g
; v n wFð0; 1Þ iid; ε n ¼ x þ l$sinh (12.7)
e n ¼ 0:7ðe n 1 þ v n Þ d
This is due to the apparent nonsignificance of any PACF coefficient for lags
greater than 1. The sensor noise is ε n , which is driven by the normally distributed
time series e n . The parameters x, l, d, and g are the Johnson system (unbounded
system) parameters corresponding to the empirical noise distributions, as shown
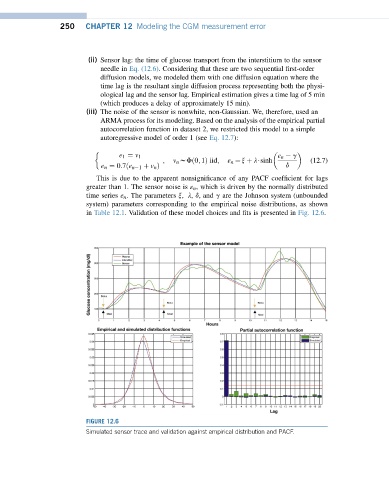
in Table 12.1. Validation of these model choices and fits is presented in Fig. 12.6.

FIGURE 12.6
Simulated sensor trace and validation against empirical distribution and PACF.