Page 766 - Handbook Of Integral Equations

Supplement 9

Tables of Inverse Mellin Transforms

See Section 8.1 of Supplement 8 for general formulas.

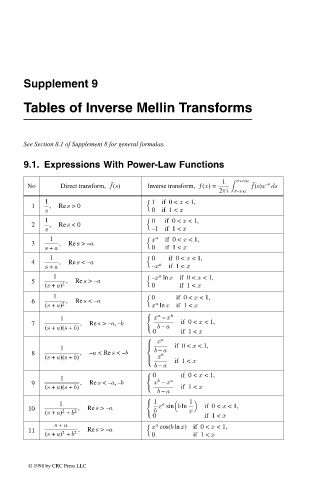
9.1. Expressions With Power-Law Functions

1 σ+i∞ –s
ˆ
ˆ
No Direct transform, f(s) Inverse transform, f(x)= f(s)x ds
2πi σ–i∞
1 1if 0 < x <1,
1 , Re s >0
s 0if 1 < x
1 0 if 0 < x <1,
2 , Re s <0
s –1if 1 < x
1 x a if 0 < x <1,
3 , Re s > –a
s + a 0 if 1 < x
1 0 if 0 < x <1,
4 , Re s < –a a
s + a –x if 1 < x
a
1 –x ln x if 0 < x <1,
5 2 , Re s > –a
(s + a) 0 if 1 < x
1 0 if 0 < x <1,
6 2 , Re s < –a a
(s + a) x ln x if 1 < x
a b
1 x – x
7 , Re s > –a, –b if 0 < x <1,
(s + a)(s + b) b – a
0 if 1 < x
x
 a
 if 0 < x <1,
1  b – a
8 , –a <Re s < –b b
(s + a)(s + b)  x
 if 1 < x
b – a
0 if 0 < x <1,

1 b a
9 , Re s < –a, –b x – x
(s + a)(s + b) if 1 < x
b – a

1 1 x sin b ln 1 if 0 < x <1,
a
10 2 2 , Re s > –a b x
(s + a) + b
0 if 1 < x
s + a x cos(b ln x)if 0 < x <1,
a
11 2 2 , Re s > –a
(s + a) + b 0 if 1 < x
© 1998 by CRC Press LLC

© 1998 by CRC Press LLC
Page 751