Page 94 - Handbook of Energy Engineering Calculations

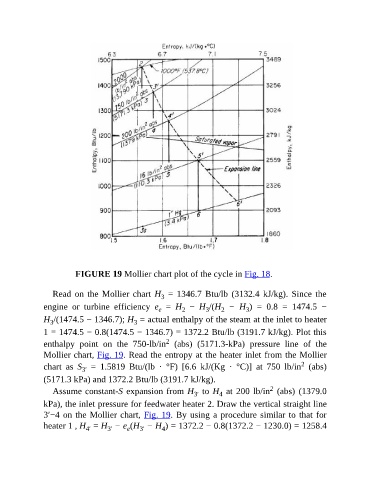
FIGURE 19 Mollier chart plot of the cycle in Fig. 18.

Read on the Mollier chart H = 1346.7 Btu/lb (3132.4 kJ/kg). Since the
3
engine or turbine efficiency e = H − H /(H − H ) = 0.8 = 1474.5 −
3
2
2
e
3
H /(1474.5 − 1346.7); H = actual enthalpy of the steam at the inlet to heater
3
3
1 = 1474.5 − 0.8(1474.5 − 1346.7) = 1372.2 Btu/lb (3191.7 kJ/kg). Plot this
2
enthalpy point on the 750-lb/in (abs) (5171.3-kPa) pressure line of the
Mollier chart, Fig. 19. Read the entropy at the heater inlet from the Mollier
2
chart as S = 1.5819 Btu/(lb · °F) [6.6 kJ/(Kg · °C)] at 750 lb/in (abs)
3′
(5171.3 kPa) and 1372.2 Btu/lb (3191.7 kJ/kg).
2
Assume constant-S expansion from H to H at 200 lb/in (abs) (1379.0
4
3′
kPa), the inlet pressure for feedwater heater 2. Draw the vertical straight line
3′−4 on the Mollier chart, Fig. 19. By using a procedure similar to that for
heater 1 , H = H − e (H − H ) = 1372.2 − 0.8(1372.2 − 1230.0) = 1258.4
3′
e
4
3′
4′