Page 203 - Handbook of Materials Failure Analysis

5 Case Study 199

M
total

M I
tower

EI

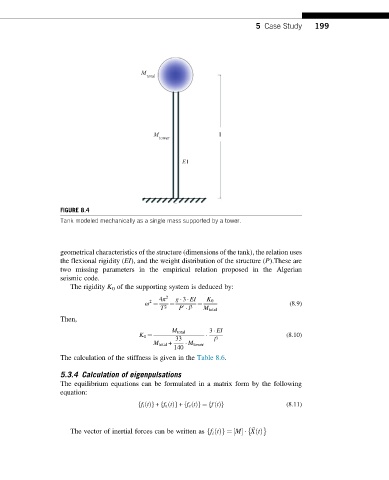
FIGURE 8.4
Tank modeled mechanically as a single mass supported by a tower.

geometrical characteristics of the structure (dimensions of the tank), the relation uses
the flexional rigidity (EI), and the weight distribution of the structure (P).These are
two missing parameters in the empirical relation proposed in the Algerian
seismic code.
The rigidity K 0 of the supporting system is deduced by:
4π 2 g 3 EI
2 K 0
T 2 P l 3 M total
ω ¼ ¼ ¼ (8.9)
0
Then,
3 EI
M total
(8.10)
33 l
K 0 ¼ 3
M total + M tower
140
The calculation of the stiffness is given in the Table 8.6.
5.3.4 Calculation of eigenpulsations
The equilibrium equations can be formulated in a matrix form by the following
equation:
(8.11)
f
f f i tðÞg + f a tðÞg + f e tðÞg ¼ ftðÞg
f
f
€

f
The vector of inertial forces can be written as f i tðÞg ¼ M½Š XtðÞ