Page 116 - Hardware Implementation of Finite-Field Arithmetic

Operations over GF ( p ) 99

a b

a b
nonrestoring start start_division
divisor
done division_done
remainder quotient
c d
r q
q c d
multiplication start start_product
and subtraction
done product_done
z
b d
next_d
load
k-bit register k-bit register 2k-bit register 2k-bit register update
initially: p initially: y initially: x initially: 0
d
a b p c
comb.
b b_equal_1
x m circ.
nonrestoring start start_reduction
reducer
done reduction_done
z
z
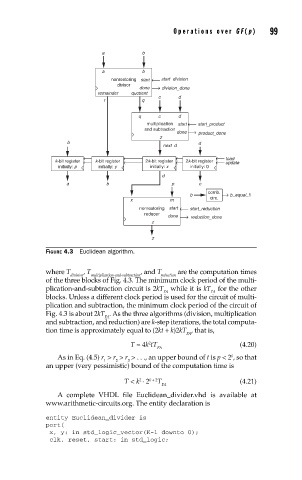
FIGURE 4.3 Euclidean algorithm.

where T , T , and T are the computation times
division multiplication-and-subtraction reduction
of the three blocks of Fig. 4.3. The minimum clock period of the multi-
plication-and-subtraction circuit is 2kT while it is kT for the other
FA FA
blocks. Unless a different clock period is used for the circuit of multi-
plication and subtraction, the minimum clock period of the circuit of
Fig. 4.3 is about 2kT . As the three algorithms (division, multiplication
FA
and subtraction, and reduction) are k-step iterations, the total computa-
tion time is approximately equal to (2kt + k)2kT , that is,
FA
T ≈ 4k tT (4.20)
2
FA
k
As in Eq. (4.5) r > r > r > . . ., an upper bound of t is p < 2 , so that
1 2 3
an upper (very pessimistic) bound of the computation time is
2 .
T < k 2 k + 2 T (4.21)
FA
A complete VHDL file Euclidean_divider.vhd is available at
www.arithmetic-circuits.org. The entity declaration is
entity Euclidean_divider is
port(
x, y: in std_logic_vector(K-1 downto 0);
clk, reset, start: in std_logic;