Page 152 - Hardware Implementation of Finite-Field Arithmetic

Operations over Z [ x ]/ f ( x ) 135
p

An executable Ada file OEF_MSE_mult.adb, including Algorithm
5.10, is available at www.arithmetic-circuits.org.
In a similar way, the LSE-first multiplication scheme given in
m
Algorithm 5.7 can be implemented for an OEF with f(x) = x – c as
follows:
Algorithm 5.11—LSE-first multiplier for OEF
for i in 0 .. m-1 loop
d := addition_mod_f_poly(product(a,b(i)),d);
a := mult_x_OEF(a,c);
end loop;
An executable Ada file OEF_LSE_mult.adb, including Algorithm 5.11,
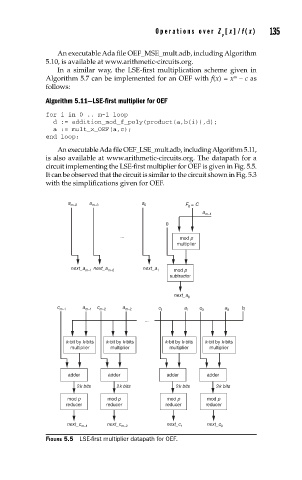
is also available at www.arithmetic-circuits.org. The datapath for a
circuit implementing the LSE-first multiplier for OEF is given in Fig. 5.5.
It can be observed that the circuit is similar to the circuit shown in Fig. 5.3
with the simplifications given for OEF.

a m–2 a m–3 a 0 F 0 = C
a m–1
0
...
mod p
multiplier

mod p
next_a m–1 next_a m–2 next_a 1
subtractor

next_a 0
c m–1 a m–1 c m–2 a m–2
c 1 a 1 c 0 a 0 b i
...

k-bit by k-bits k-bit by k-bits k-bit by k-bits k-bit by k-bits
multiplier multiplier multiplier multiplier

adder adder adder adder
2k bits 2k bits 2k bits 2k bits
mod p mod p mod p mod p
reducer reducer reducer reducer

next_c m–1 next_c m–2 next_c 1 next_c 0
FIGURE 5.5 LSE-fi rst multiplier datapath for OEF.