Page 268 - Hardware Implementation of Finite-Field Arithmetic

248 Cha pte r Ei g h t

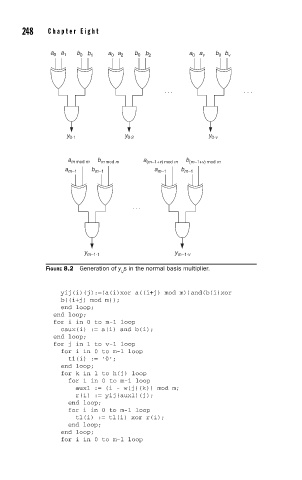
a 0 a 1 b 0 b 1 a 0 a 2 b 0 b 2 a 0 a v b 0 b v

. . . . . .

y 0·1 y 0·2 y 0·v

a m mod m b m mod m a (m–1+v) mod m b (m–1+v) mod m
a m–1 b m–1 a m–1 b m–1

. . .

y m–1·1 y m–1·v
FIGURE 8.2 Generation of y s in the normal basis multiplier.
i,j

yij(i)(j):=(a(i)xor a((i+j) mod m))and(b(i)xor
b((i+j) mod m));
end loop;
end loop;
for i in 0 to m-1 loop
caux(i) := a(i) and b(i);
end loop;
for j in 1 to v-1 loop
for i in 0 to m-1 loop
t1(i) := ‘0’;
end loop;
for k in 1 to h(j) loop
for i in 0 to m-1 loop
aux1 := (i - w(j)(k)) mod m;
r(i) := yij(aux1)(j);
end loop;
for i in 0 to m-1 loop
t1(i) := t1(i) xor r(i);
end loop;
end loop;
for i in 0 to m-1 loop