Page 286 - Hardware Implementation of Finite-Field Arithmetic

266 Cha pte r Ei g h t

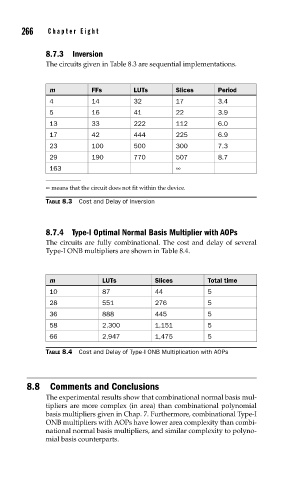
8.7.3 Inversion
The circuits given in Table 8.3 are sequential implementations.

m FFs LUTs Slices Period
4 14 32 17 3.4
5 16 41 22 3.9
13 33 222 112 6.0
17 42 444 225 6.9
23 100 500 300 7.3
29 190 770 507 8.7
163 ∞

∞ means that the circuit does not fit within the device.
TABLE 8.3 Cost and Delay of Inversion

8.7.4 Type-I Optimal Normal Basis Multiplier with AOPs
The circuits are fully combinational. The cost and delay of several
Type-I ONB multipliers are shown in Table 8.4.

m LUTs Slices Total time
10 87 44 5
28 551 276 5
36 888 445 5
58 2,300 1,151 5
66 2,947 1,475 5

TABLE 8.4 Cost and Delay of Type-I ONB Multiplication with AOPs

8.8 Comments and Conclusions
The experimental results show that combinational normal basis mul-
tipliers are more complex (in area) than combinational polynomial
basis multipliers given in Chap. 7. Furthermore, combinational Type-I
ONB multipliers with AOPs have lower area complexity than combi-
national normal basis multipliers, and similar complexity to polyno-
mial basis counterparts.