Page 352 - Hardware Implementation of Finite-Field Arithmetic

332 App endix C

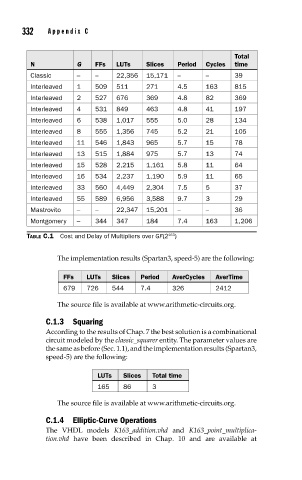
Total
N G FFs LUTs Slices Period Cycles time
Classic – – 22,356 15,171 – – 39
Interleaved 1 509 511 271 4.5 163 815
Interleaved 2 527 676 369 4.8 82 369
Interleaved 4 531 849 463 4.8 41 197
Interleaved 6 538 1,017 555 5.0 28 134
Interleaved 8 555 1,356 745 5.2 21 105
Interleaved 11 546 1,843 965 5.7 15 78
Interleaved 13 515 1,884 975 5.7 13 74
Interleaved 15 528 2,215 1,161 5.8 11 64
Interleaved 16 534 2,237 1,190 5.9 11 65
Interleaved 33 560 4,449 2,304 7.5 5 37
Interleaved 55 589 6,956 3,588 9.7 3 29
Mastrovito – – 22,347 15,201 – – 36
Montgomery – 344 347 184 7.4 163 1,206

TABLE C.1 Cost and Delay of Multipliers over GF(2 163 )

The implementation results (Spartan3, speed-5) are the following:

FFs LUTs Slices Period AverCycles AverTime
679 726 544 7.4 326 2412
The source file is available at www.arithmetic-circuits.org.

C.1.3 Squaring
According to the results of Chap. 7 the best solution is a combinational
circuit modeled by the classic_squarer entity. The parameter values are
the same as before (Sec. 1.1), and the implementation results (Spartan3,
speed-5) are the following:

LUTs Slices Total time
165 86 3
The source file is available at www.arithmetic-circuits.org.

C.1.4 Elliptic-Curve Operations
The VHDL models K163_addition.vhd and K163_point_multiplica-
tion.vhd have been described in Chap. 10 and are available at