Page 191 - How To Solve Word Problems In Calculus

P1: FYN/FZQ P2: FXS
PB056-07 Macros-FMT June 1, 2001 13:49 Char Count= 0

If f (x) is negative over all or part of [a, b], the integral
b

f (x) dx will not give the desired area; the area must be de-
a
b

termined by computing | f (x)| dx. Since the Fundamental
a
Theorem of Calculus cannot be conveniently applied to a
function involving an absolute value, one must first deter-
mine where the graph crosses the x axis, break up the interval
into subintervals determined by these points, integrate sepa-
rately in each subinterval, and add the absolute values of the
integrals. The next example illustrates this procedure.

EXAMPLE 3
2
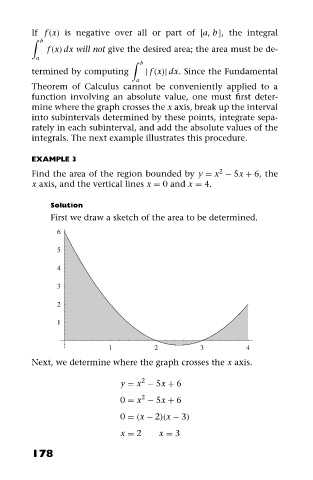
Find the area of the region bounded by y = x − 5x + 6, the
x axis, and the vertical lines x = 0 and x = 4.

Solution
First we draw a sketch of the area to be determined.
6 6

5 5

4 4

3 3

2 2
1 1

1 1 2 2 3 3 4 4

Next, we determine where the graph crosses the x axis.

2
y = x − 5x + 6
2
0 = x − 5x + 6
0 = (x − 2)(x − 3)

x = 2 x = 3

178