Page 196 - How To Solve Word Problems In Calculus

P1: FYN/FZQ P2: FXS
PB056-07 Macros-FMT June 1, 2001 13:49 Char Count= 0

Solution

2 2

1 1 (x,y)
1
(x,y)
2

1 1 2 2 3 3 4 4

− 1
−1

− 2
−2

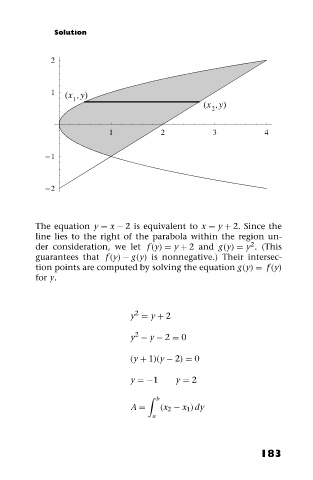
The equation y = x − 2 is equivalent to x = y + 2. Since the
line lies to the right of the parabola within the region un-
2
der consideration, we let f (y) = y + 2 and g(y) = y . (This
guarantees that f (y) − g(y) is nonnegative.) Their intersec-
tion points are computed by solving the equation g(y) = f (y)
for y.

2
y = y + 2
2
y − y − 2 = 0

(y + 1)(y − 2) = 0

y =−1 y = 2

b

A = (x 2 − x 1 ) dy
a

183