Page 196 - Hybrid-Renewable Energy Systems in Microgrids

176 Hybrid-Renewable Energy Systems in Microgrids

2.4.1 Drive train

Three drive train parameters such as shaft stiffness, turbine inertia, and generator iner-
tia are considered for sensitivity analysis. For each analysis the other parameters are
kept constant.
Shaft Stiffness: Table 9.1 shows that the incorporation of SDBR has not much con-
tribution on the damping of the mechanical mode. On the other hand, it has significant
improvement in case of other electrical modes. The sensitivity of mechanical modes
with respect to shaft stiffness is given by the following:

∂ λ ∂ λ ∂a ∂ λ ∂a
∂λ ∂Ks=∂λ ∂a3,2.∂a3,2∂Ks+ 9 = 9 . 3,2 + 9 . 1,2 (9.32)
9
9
∂λ ∂a1,2.∂a1,2∂Ks ∂K s ∂a 3,2 ∂K s ∂a 1,2 ∂K s
9
a , a are computed from the state matrix A and listed in appendix.
1,2
3,2
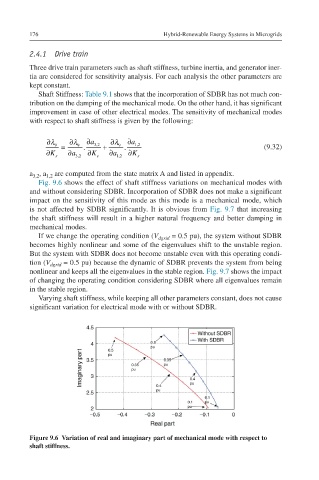
Fig. 9.6 shows the effect of shaft stiffness variations on mechanical modes with
and without considering SDBR. Incorporation of SDBR does not make a significant
impact on the sensitivity of this mode as this mode is a mechanical mode, which
is not affected by SDBR significantly. It is obvious from Fig. 9.7 that increasing
the shaft stiffness will result in a higher natural frequency and better damping in
mechanical modes.
If we change the operating condition (V dgrid = 0.5 pu), the system without SDBR
becomes highly nonlinear and some of the eigenvalues shift to the unstable region.
But the system with SDBR does not become unstable even with this operating condi-
tion (V dgrid = 0.5 pu) because the dynamic of SDBR prevents the system from being
nonlinear and keeps all the eigenvalues in the stable region. Fig. 9.7 shows the impact
of changing the operating condition considering SDBR where all eigenvalues remain
in the stable region.
Varying shaft stiffness, while keeping all other parameters constant, does not cause
significant variation for electrical mode with or without SDBR.

Figure 9.6 Variation of real and imaginary part of mechanical mode with respect to
shaft stiffness.