Page 315 - Hydrogeology Principles and Practice

HYDC08 12/5/05 5:31 PM Page 298

298 Chapter Eight

Computation of the rate and volume of stream depletion by BO X
boreholes and wells 8.4

The following example illustrates the application of an analytical S, specific yield = 0.20
solution to the problem of stream flow depletion caused by ground- Qt, net volume of water pumped = (0.03 m s ) × (200 days) ×
3 −1
water abstraction. The solution uses one of the type curves and 5 3
tables presented by Jenkins (1968) to assist the calculation of the (86,400 seconds per day) = 5.184 × 10 m
rate and volume of stream flow depletion.
The problem to be solved is as follows. A new borehole is to be As a first step, compute v/Qt, the dimensionless ratio of the volume
drilled for supporting municipal water supply from an unconfined of stream depletion to volume of water pumped for the pumping
alluvial aquifer close to a stream. The alluvial aquifer has a trans- period of interest which, in our example is equal to 5000/5.184 ×
5
2 −1
−3
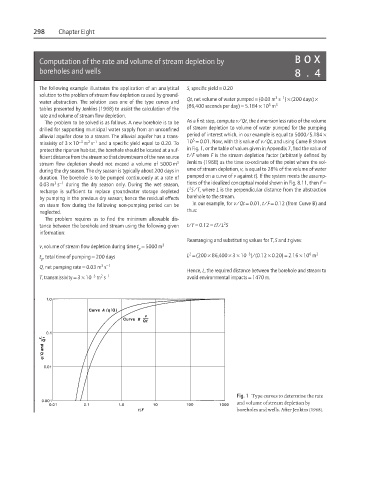
missivity of 3 × 10 m s and a specific yield equal to 0.20. To 10 = 0.01. Now, with this value of v/Qt, and using Curve B shown
protect the riparian habitat, the borehole should be located at a suf- in Fig. 1, or the table of values given in Appendix 7, find the value of
ficient distance from the stream so that downstream of the new source t/F where F is the stream depletion factor (arbitrarily defined by
stream flow depletion should not exceed a volume of 5000 m 3 Jenkins (1968) as the time co-ordinate of the point where the vol-
during the dry season. The dry season is typically about 200 days in ume of stream depletion, v, is equal to 28% of the volume of water
duration. The borehole is to be pumped continuously at a rate of pumped on a curve of v against t). If the system meets the assump-
3 −1
0.03 m s during the dry season only. During the wet season, tions of the idealized conceptual model shown in Fig. 8.11, then F =
2
recharge is sufficient to replace groundwater storage depleted L S/T, where L is the perpendicular distance from the abstraction
by pumping in the previous dry season; hence the residual effects borehole to the stream.
on steam flow during the following non-pumping period can be In our example, for v/Qt = 0.01, t/F = 0.12 (from Curve B) and
neglected. thus:
The problem requires us to find the minimum allowable dis-
2
tance between the borehole and stream using the following given t/F = 0.12 = tT/L S
information:
Rearranging and substituting values for T, S and t gives:
v, volume of stream flow depletion during time t = 5000 m 3
p
2
6
−3
t , total time of pumping = 200 days L = (200 × 86,400 × 3 × 10 )/(0.12 × 0.20) = 2.16 × 10 m 2
p
3 −1
Q, net pumping rate = 0.03 m s
Hence, L, the required distance between the borehole and stream to
2 −1
−3
T, transmissivity = 3 × 10 m s avoid environmental impacts = 1470 m.

Fig. 1 Type curves to determine the rate
and volume of stream depletion by
boreholes and wells. After Jenkins (1968).