Page 82 - Introduction to Computational Fluid Dynamics
P. 82
P2: IWV
P1: KsF/ICD/GKJ
CB908/Date
0 521 85326 5
0521853265c03
3.6 NUMERICAL FALSE DIFFUSION
CDS May 25, 2005 10:54 61
EXACT
1.0
Φ P
UDS
0.0
−10 −5 0 5 10
P c
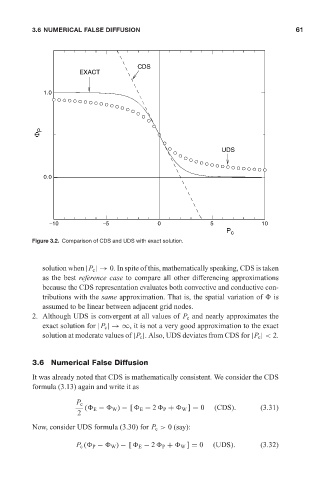
Figure 3.2. Comparison of CDS and UDS with exact solution.
solution when |P c |→ 0. In spite of this, mathematically speaking, CDS is taken
as the best reference case to compare all other differencing approximations
because the CDS representation evaluates both convective and conductive con-
tributions with the same approximation. That is, the spatial variation of is
assumed to be linear between adjacent grid nodes.
2. Although UDS is convergent at all values of P c and nearly approximates the
exact solution for |P c |→∞, it is not a very good approximation to the exact
solution at moderate values of |P c |. Also, UDS deviates from CDS for |P c | < 2.
3.6 Numerical False Diffusion
It was already noted that CDS is mathematically consistent. We consider the CDS
formula (3.13) again and write it as
P c
( E − W ) − [ E − 2 P + W ] = 0 (CDS). (3.31)
2
Now, consider UDS formula (3.30) for P c > 0 (say):
P c ( P − W ) − [ E − 2 P + W ] = 0 (UDS). (3.32)