Page 137 - Introduction to Mineral Exploration

120 M.K.G. WHATELEY

A B Photograph 1
Negative
f
L Lens Top

(H-h)=H′
H Base
a b
Ground level
h
Sea level
P 1 P
FIG. 6.9 The factors used to calculate the scale of PX 2
aerial photographs. (Modified after Allum 1966.) 1
PX 4
In vertical photographs taken over flat ter-
rain, scale (S) is a function of the focal length (f)
of the camera and the flying height above the Photograph 2
ground (H′) of the aircraft (Fig. 6.9).
Top
f
=
Scale( )
S
H′ Base
H′ is obtained by subtracting the terrain eleva-
tion (h) from the height of the aircraft above a
datum (H), usually sea level which is the value
given by the aircraft’s altimeter. The import- P 1 P 2 P 3
ant principle to understand is that photograph
PX 2
scale is a function of terrain elevation. A plane
flies at a constant (or nearly constant) height.
When a plane flies over varying terrain eleva- PX 3
tion, such as in mountainous areas, then the
scale will vary rapidly across the photographs.
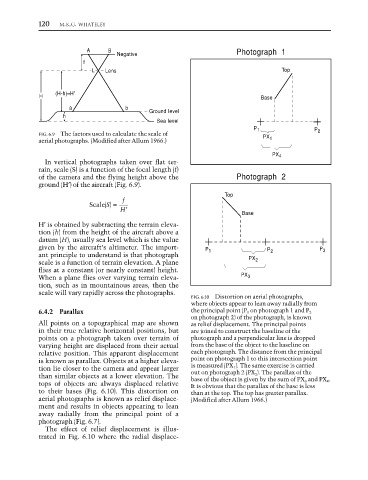
FIG. 6.10 Distortion on aerial photographs,
where objects appear to lean away radially from
6.4.2 Parallax the principal point (P 1 on photograph 1 and P 2
on photograph 2) of the photograph, is known
All points on a topographical map are shown as relief displacement. The principal points
in their true relative horizontal positions, but are joined to construct the baseline of the
points on a photograph taken over terrain of photograph and a perpendicular line is dropped
varying height are displaced from their actual from the base of the object to the baseline on
relative position. This apparent displacement each photograph. The distance from the principal
is known as parallax. Objects at a higher eleva- point on photograph 1 to this intersection point
tion lie closer to the camera and appear larger is measured (PX 1 ). The same exercise is carried
than similar objects at a lower elevation. The out on photograph 2 (PX 2 ). The parallax of the
base of the object is given by the sum of PX 3 and PX 4 .
tops of objects are always displaced relative It is obvious that the parallax of the base is less
to their bases (Fig. 6.10). This distortion on than at the top. The top has greater parallax.
aerial photographs is known as relief displace- (Modified after Allum 1966.)
ment and results in objects appearing to lean
away radially from the principal point of a
photograph (Fig. 6.7).
The effect of relief displacement is illus-
trated in Fig. 6.10 where the radial displace-