Page 322 - Materials Chemistry, Second Edition

15.4 Results and discussion 321
0:2348 + 4 0:2753 + 0:3101
ω T 2 ¼ ¼ 0:2744 (15.24)
6
EC 3
0:1001 + 4 0:1053 + 0:1122
ω T 2 ¼ ¼ 0:1056 (15.25)
6
SM 1
0:1511 + 4 0:1689 + 0:2096
ω T 2 ¼ ¼ 0:1727 (15.26)
6
SM 2

Substep 5: Consistency check.
The consistency ratio can be determined by Eq. (15.27).
ξ ∗ 0:4074
CR ¼ ¼ ¼ 0:0507 (15.27)
CI 8:04
It is apparent that CR is less than 0.10; thus, the consistency of these judgments is accept-
able, and the judgments of the experts for determining the weights (relative influences) of
these four influential factors are effective.
In a similar way, the relative influences of the influential factors on each factor can be de-
termined, and the results are presented in the Appendix. The initial influential matrix can
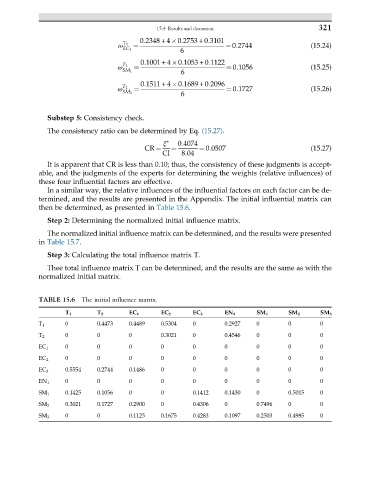
then be determined, as presented in Table 15.6.
Step 2: Determining the normalized initial influence matrix.
The normalized initial influence matrix can be determined, and the results were presented
in Table 15.7.
Step 3: Calculating the total influence matrix T.
Thee total influence matrix T can be determined, and the results are the same as with the
normalized initial matrix.

TABLE 15.6 The initial influence matrix.
T 1 T 2 EC 1 EC 2 EC 3 EN 1 SM 1 SM 2 SM 3
0 0.4473 0.4489 0.5304 0 0.2927 0 0 0
T 1
0 0 0 0.3021 0 0.4546 0 0 0
T 2
0 0 0 0 0 0 0 0 0
EC 1
0 0 0 0 0 0 0 0 0
EC 2
0.5554 0.2744 0.1486 0 0 0 0 0 0
EC 3
EN 1 0 0 0 0 0 0 0 0 0
SM 1 0.1425 0.1056 0 0 0.1412 0.1430 0 0.5015 0
SM 2 0.3021 0.1727 0.2900 0 0.4306 0 0.7496 0 0
SM 3 0 0 0.1125 0.1675 0.4283 0.1097 0.2503 0.4985 0