Page 317 - MATLAB an introduction with applications
P. 317
302 ——— MATLAB: An Introduction with Applications
input data
6
5
4
3
2
1
0
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
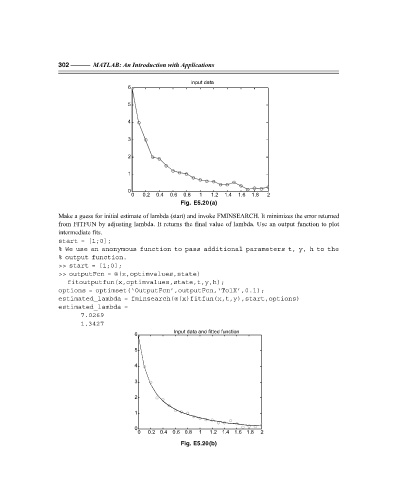
Fig. E5.20 (a)
Make a guess for initial estimate of lambda (start) and invoke FMINSEARCH. It minimizes the error returned
from FITFUN by adjusting lambda. It returns the final value of lambda. Use an output function to plot
intermediate fits.
start = [1;0];
% We use an anonymous function to pass additional parameters t, y, h to the
% output function.
>> start = [1;0];
>> outputFcn = @(x,optimvalues,state)
fitoutputfun(x,optimvalues,state,t,y,h);
options = optimset(‘OutputFcn’,outputFcn,‘TolX’,0.1);
estimated_lambda = fminsearch(@(x)fitfun(x,t,y),start,options)
estimated_lambda =
7.0269
1.3427
Input data and fitted function
6
5
4
3
2
1
0
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
Fig. E5.20(b)