Page 170 - Machine Learning for Subsurface Characterization

144 Machine learning for subsurface characterization

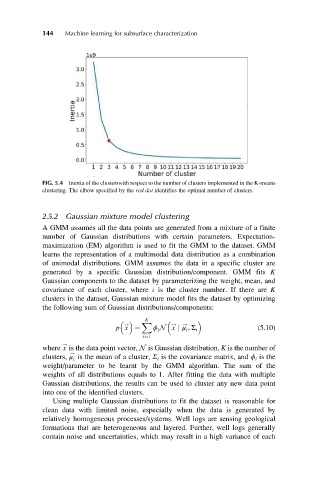
FIG. 5.4 Inertia of the clusterswith respect to the number of clusters implemented in the K-means
clustering. The elbow specified by the red dot identifies the optimal number of clusters.

2.5.2 Gaussian mixture model clustering
A GMM assumes all the data points are generated from a mixture of a finite
number of Gaussian distributions with certain parameters. Expectation-
maximization (EM) algorithm is used to fit the GMM to the dataset. GMM
learns the representation of a multimodal data distribution as a combination
of unimodal distributions. GMM assumes the data in a specific cluster are
generated by a specific Gaussian distribution/component. GMM fits K
Gaussian components to the dataset by parameterizing the weight, mean, and
covariance of each cluster, where i is the cluster number. If there are K
clusters in the dataset, Gaussian mixture model fits the dataset by optimizing
the following sum of Gaussian distributions/components:

K

X
! ! !
px ¼ ϕ N x j μ , Σ i (5.10)
i
i
i¼1
!
where x is the data point vector, N is Gaussian distribution, K is the number of
!
clusters, μ is the mean of a cluster, Σ i is the covariance matrix, and ϕ i is the
i
weight/parameter to be learnt by the GMM algorithm. The sum of the
weights of all distributions equals to 1. After fitting the data with multiple
Gaussian distributions, the results can be used to cluster any new data point
into one of the identified clusters.
Using multiple Gaussian distributions to fit the dataset is reasonable for
clean data with limited noise, especially when the data is generated by
relatively homogeneous processes/systems. Well logs are sensing geological
formations that are heterogeneous and layered. Further, well logs generally
contain noise and uncertainties, which may result in a high variance of each