Page 171 - Machine Learning for Subsurface Characterization

Robust geomechanical characterization Chapter 5 145

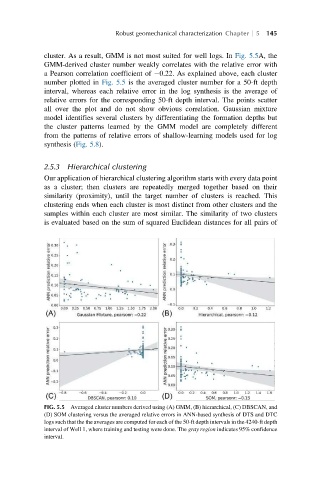
cluster. As a result, GMM is not most suited for well logs. In Fig. 5.5A, the
GMM-derived cluster number weakly correlates with the relative error with
a Pearson correlation coefficient of 0.22. As explained above, each cluster
number plotted in Fig. 5.5 is the averaged cluster number for a 50-ft depth
interval, whereas each relative error in the log synthesis is the average of
relative errors for the corresponding 50-ft depth interval. The points scatter
all over the plot and do not show obvious correlation. Gaussian mixture
model identifies several clusters by differentiating the formation depths but
the cluster patterns learned by the GMM model are completely different
from the patterns of relative errors of shallow-learning models used for log
synthesis (Fig. 5.8).

2.5.3 Hierarchical clustering
Our application of hierarchical clustering algorithm starts with every data point
as a cluster; then clusters are repeatedly merged together based on their
similarity (proximity), until the target number of clusters is reached. This
clustering ends when each cluster is most distinct from other clusters and the
samples within each cluster are most similar. The similarity of two clusters
is evaluated based on the sum of squared Euclidean distances for all pairs of

FIG. 5.5 Averaged cluster numbers derived using (A) GMM, (B) hierarchical, (C) DBSCAN, and
(D) SOM clustering versus the averaged relative errors in ANN-based synthesis of DTS and DTC
logs such that the the averages are computed for each of the 50-ft depth intervals in the 4240-ft depth
interval of Well 1, where training and testing were done. The gray region indicates 95% confidence
interval.