Page 143 - Macromolecular Crystallography

132 MACROMOLECULAR CRYS TALLOGRAPHY

Table 9.3 Number of peak-wavelength anomalous difference data 1.00
pairs for 1JC4 remaining after successive application of the various
DIFFE significance tests A = 6
A = 4
Number
0.75
Unique reflection data (|E|) 66, 122
Total anomalous reflection pairs (|E D |) 28, 399
A = 2
Data pairs passing T MAX test 28, 364
Data pairs passing X MIN test 26, 898 P (Φ HK ) 0.50
Data pairs passing Y MIN test 13, 790
A = 1
Data pairs passing Z MIN and Z MAX tests 2474

0.25
4. Normalized |E | are excluded if |E |/σ(|E |)< A = 0
Z MIN (3.0). A = 1
A = 4
5. Normalized |E | are excluded if [|E |− A = 2
0.00
|E | MAX ]/σ(|E |)> Z MAX (0.0). –200 –100 0 100 200
Φ HK = φ +φ + φ -H-K
K
H
The parameter T MAX is used to reject data with
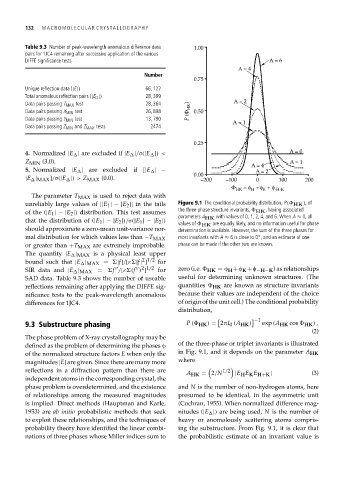
unreliably large values of ||E 1 |−|E 2 || in the tails Figure 9.1 The conditional probability distribution, P( HK ),of
the three-phase structure invariants, HK , having associated
of the (|E 1 |−|E 2 |) distribution. This test assumes
parameters A HK with values of 0, 1, 2, 4, and 6. When A ≈ 0, all
that the distribution of (|E 1 |−|E 2 |)/σ(|E 1 |−|E 2 |)
values of HK are equally likely, and no information useful for phase
should approximate a zero-mean unit-variance nor- determination is available. However, the sum of the three phases for
◦
mal distribution for which values less than −T MAX most invariants with A ≈ 6 is close to 0 , and an estimate of one
or greater than +T MAX are extremely improbable. phase can be made if the other two are known.
The quantity |E | MAX is a physical least upper
2 1/2
bound such that |E | MAX = |f|/[ε |f| ] for
2 1/2 zero (i.e. HK = φ H +φ K +φ −H−K ) as relationships
SIR data and |E | MAX = f /[ε (f ) ] for
SAD data. Table 9.3 shows the number of useable useful for determining unknown structures. (The
reflections remaining after applying the DIFFE sig- quantities HK are known as structure invariants
nificance tests to the peak-wavelength anomalous because their values are independent of the choice
differences for 1JC4. of origin of the unit cell.) The conditional probability
distribution,
−1
9.3 Substructure phasing P ( HK ) = 2πI 0 (A HK ) exp (A HK cos HK ) ,
(2)
The phase problem of X-ray crystallography may be
defined as the problem of determining the phases φ of the three-phase or triplet invariants is illustrated
of the normalized structure factors E when only the in Fig. 9.1, and it depends on the parameter A HK
magnitudes |E| are given. Since there are many more where
reflections in a diffraction pattern than there are 1/2
A HK = 2/N |E H E K E H+K | (3)
independent atoms in the corresponding crystal, the
phase problem is overdetermined, and the existence and N is the number of non-hydrogen atoms, here
of relationships among the measured magnitudes presumed to be identical, in the asymmetric unit
is implied. Direct methods (Hauptman and Karle, (Cochran, 1955). When normalized difference mag-
1953) are ab initio probabilistic methods that seek nitudes (|E |) are being used, N is the number of
to exploit these relationships, and the techniques of heavy or anomalously scattering atoms compris-
probability theory have identified the linear combi- ing the substructure. From Fig. 9.1, it is clear that
nations of three phases whose Miller indices sum to the probabilistic estimate of an invariant value is