Page 160 - Macromolecular Crystallography

PHASE REFINEMENT THROUGH DENSITY MODIFICATION 149

(a) F init (h) is the Fourier transform of the unmodified
density map, ρ init (x).
G(h) is the Fourier transform of the protein mask,
often referred to as an interference function.
C(h) defines a small correction, mainly peaking at
the origin.
Applying a mask function in real space is equiv-
alent to combining many structure factors through
(b) a convolution in reciprocal space. This results in an
improvement because the random error component
of the structure factors will average out, whereas
the true values of the structure factors will add up
systematically. Fig. 10.4 gives a graphical example
showing this phenomenon.
As is described in Abrahams (1997), plotting the
radial distribution of the intensity of the interfer-
ence function G(h), most of the intensity is around
(c)
the origin. Thus, when you convolute the struc-
ture factors F with the interference function G, each
structure factor will mainly be recombined with
structure factors that are close by.
However, this procedure is not entirely without
problems. Importantly, there is a term in the con-
volution given in Eq. 9 which cannot be neglected:
it is the value of the G(a) function at (h = 0). The
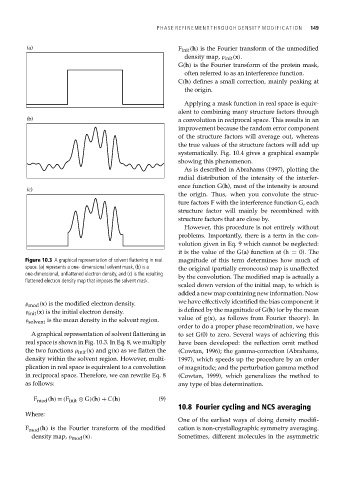
Figure 10.3 A graphical representation of solvent flattening in real magnitude of this term determines how much of
space. (a) represents a one- dimensional solvent mask, (b) is a the original (partially erroneous) map is unaffected
one-dimensional, unflattened electron density, and (c) is the resulting by the convolution. The modified map is actually a
flattened electron density map that imposes the solvent mask.
scaled down version of the initial map, to which is
added a new map containing new information. Now
ρ mod (x) is the modified electron density. we have effectively identified the bias component: it
ρ init (x) is the initial electron density. is defined by the magnitude of G(h) (or by the mean
ρ solvent is the mean density in the solvent region. value of g(x), as follows from Fourier theory). In
order to do a proper phase recombination, we have
A graphical representation of solvent flattening in to set G(0) to zero. Several ways of achieving this
real space is shown in Fig. 10.3. In Eq. 8, we multiply have been developed: the reflection omit method
the two functions ρ init (x) and g(x) as we flatten the (Cowtan, 1996); the gamma-correction (Abrahams,
density within the solvent region. However, multi- 1997), which speeds up the procedure by an order
plication in real space is equivalent to a convolution of magnitude; and the perturbation gamma method
in reciprocal space. Therefore, we can rewrite Eq. 8 (Cowtan, 1999), which generalizes the method to
as follows: any type of bias determination.

F mod (h) = (F init ⊗ G)(h) + C(h) (9)
10.8 Fourier cycling and NCS averaging
Where:
One of the earliest ways of doing density modifi-
F mod (h) is the Fourier transform of the modified cation is non-crystallographic symmetry averaging.
density map, ρ mod (x). Sometimes, different molecules in the asymmetric