Page 86 - 04. Subyek Engineering Materials - Manufacturing, Engineering and Technology SI 6th Edition - Serope Kalpakjian, Stephen Schmid (2009)

TABLE 2.4
Typical Ranges of Strain and Deformation Rate in Manufacturing Processes
Process True strain Deformation rate (m/s)
Cold working
Forging, rolling 0.1-0.5 0.1-100
Wire and tube drawing 0.05-0.5 0.1-100
Explosive forming 0.05-0.2 10-100
Hot working and warm working
Forging, rolling 0.1-0.5 0.1-30
Extrusion 2-5 0.1-1
Machining 1-10 0.1-100
Sheet-metal forming 0.1-0.5 0.05-2
Superplastic forming 0.2-3 104'-10'2

the specimen’s length. A short specimen elongates proportionately more during the
same period than does a long specimen. For example, let’s take two rubber bands,
one 20 mm and the other 100 mm long, respectively, and elongate them both by 10
mm within a period of 1 second. The engineering strain in the shorter specimen is
% = 0.5; that in the longer is % = 0.1. Thus, the strain rates are 0.5 ST1 and 0.1 s`1,
respectively, with the short band being subjected to a strain rate five times higher than
that for the long band, although they are both being stretched at the same deforma-
tion rate.
Deformation rates typically employed in various testing and metalworking
processes, and the true strains involved, are given in Table 2.4. Because of the wide
range encountered in practice, strain rates are usually
stated in terms of orders of magnitude, such as 102 s`l, Room 30°C
104 ST1, and so on. 200 _iempelamre
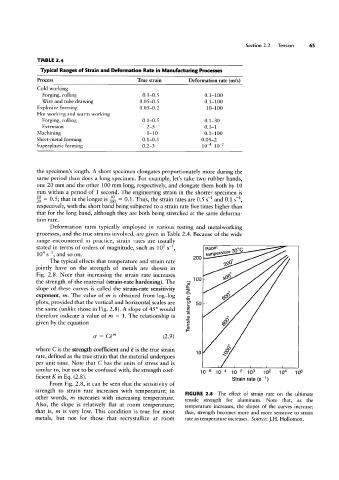
The typical effects that temperature and strain rate T 200°
jointly have on the strength of metals are shown in
Fig. 2.8. Note that increasing the strain rate increases 5967
the strength of the material (strain-rate hardening). The 1; 100
slope of these curves is called the strain-rate sensitivity Q O
exponent, m. The value of m is obtained from log-log fi 69°
plots, provided that the vertical and horizontal scales are E’ 50 -
the same (unlike those in Fig. 2.8). A slope of 45° would 2
therefore indicate a value of m = 1. The relationship is Q 8
given by the equation Q9
3
rr = Cém (2.9)
§
where C is the strength coefficient and é is the true strain 10
rate, defined as the true strain that the material undergoes "
per unit time. Note that C has the units of stress and is
similar to, but not to be confused with, the strength coef- 10'610'410'2100 102 104 105
ficient K in Eq. (2.8). Strain rate (s")
From Fig. 2.8, it can be seen that the sensitivity of
strength to strain rate increases with temperature; in
FIGURE 2.8 The effect of strain rate on the ultimate
other words, m increases with increasing temperature.
tensile strength for aluminum. Note that, as the
Also, the slope is relatively flat at room temperature; temperature increases, the slopes of the curves increase;
that is, m is very low. This condition is true for most thus, strength becomes more and more sensitive to strain
metals, but not for those that recrystallize at room rate as temperature increases. Source: ].H. Hollomon.