Page 290 - Materials Science and Engineering An Introduction

262 • Chapter 8 / Failure

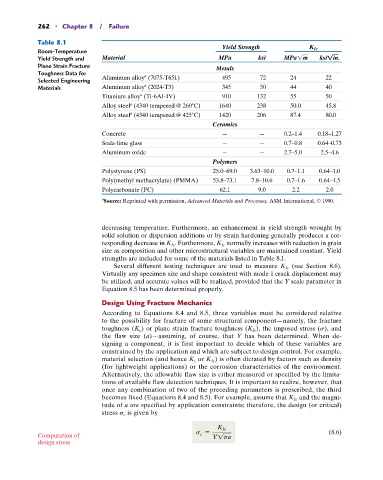
Table 8.1
Yield Strength K Ic
Room-Temperature
Yield Strength and Material MPa ksi MPa1m ksi!in.
Plane Strain Fracture Metals
Toughness Data for a
Selected Engineering Aluminum alloy (7075-T651) 495 72 24 22
a
Materials Aluminum alloy (2024-T3) 345 50 44 40
Titanium alloy (Ti-6Al-4V) 910 132 55 50
a
Alloy steel (4340 tempered @ 260 C) 1640 238 50.0 45.8
a
Alloy steel (4340 tempered @ 425 C) 1420 206 87.4 80.0
a
Ceramics
Concrete — — 0.2–1.4 0.18–1.27
Soda-lime glass — — 0.7–0.8 0.64–0.73
Aluminum oxide — — 2.7–5.0 2.5–4.6
Polymers
Polystyrene (PS) 25.0–69.0 3.63–10.0 0.7–1.1 0.64–1.0
Poly(methyl methacrylate) (PMMA) 53.8–73.1 7.8–10.6 0.7–1.6 0.64–1.5
Polycarbonate (PC) 62.1 9.0 2.2 2.0
a
Source: Reprinted with permission, Advanced Materials and Processes, ASM International, © 1990.

decreasing temperature. Furthermore, an enhancement in yield strength wrought by
solid solution or dispersion additions or by strain hardening generally produces a cor-
responding decrease in K Ic . Furthermore, K Ic normally increases with reduction in grain
size as composition and other microstructural variables are maintained constant. Yield
strengths are included for some of the materials listed in Table 8.1.
(see Section 8.6).
Several different testing techniques are used to measure K Ic
Virtually any specimen size and shape consistent with mode I crack displacement may
be utilized, and accurate values will be realized, provided that the Y scale parameter in
Equation 8.5 has been determined properly.
Design Using Fracture Mechanics
According to Equations 8.4 and 8.5, three variables must be considered relative
to the possibility for fracture of some structural component—namely, the fracture
toughness (K c ) or plane strain fracture toughness (K Ic ), the imposed stress (s), and
the flaw size (a)—assuming, of course, that Y has been determined. When de-
signing a component, it is first important to decide which of these variables are
c onstrained by the application and which are subject to design control. For example,
material selection (and hence K c or K Ic ) is often dictated by factors such as density
(for lightweight applications) or the corrosion characteristics of the environment.
Alternatively, the allowable flaw size is either measured or specified by the limita-
tions of available flaw detection techniques. It is important to realize, however, that
once any combination of two of the preceding parameters is prescribed, the third
becomes fixed (Equations 8.4 and 8.5). For example, assume that K Ic and the magni-
tude of a are specified by application constraints; therefore, the design (or critical)
stress c is given by

s c = K Ic (8.6)
Computation of Y1pa
design stress