Page 312 - Materials Science and Engineering An Introduction

284 • Chapter 8 / Failure

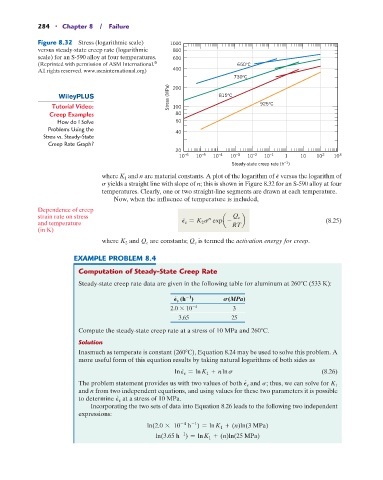
Figure 8.32 Stress (logarithmic scale) 1000
versus steady-state creep rate (logarithmic 800
scale) for an S-590 alloy at four temperatures. 600
®
(Reprinted with permission of ASM International. 650°C
All rights reserved. www.asminternational.org) 400
730°C
Stress (MPa) 200 815°C

Tutorial Video: 100 925°C
Creep Examples 80
How do I Solve 60
Problems Using the 40
Stress vs. Steady-State
Creep Rate Graph?
20
10 –6 10 –5 10 –4 10 –3 10 –2 10 –1 1 10 10 2 10 3
–1
Steady-state creep rate (h )
#
where K 1 and n are material constants. A plot of the logarithm of P versus the logarithm of
s yields a straight line with slope of n; this is shown in Figure 8.32 for an S-590 alloy at four
temperatures. Clearly, one or two straight-line segments are drawn at each temperature.
Now, when the influence of temperature is included,
Dependence of creep
strain rate on stress # n Q c
and temperature P s = K 2 s expa - RT b (8.25)
(in K)
where K 2 and Q c are constants; Q c is termed the activation energy for creep.

EXAMPLE PROBLEM 8.4
Computation of Steady-State Creep Rate
Steady-state creep rate data are given in the following table for aluminum at 260 C (533 K):

# -1
` s (h ) S(MPa)
2.0 10 4 3
3.65 25
Compute the steady-state creep rate at a stress of 10 MPa and 260 C.

Solution
Inasmuch as temperate is constant (260 C), Equation 8.24 may be used to solve this problem. A
more useful form of this equation results by taking natural logarithms of both sides as
#
ln P s = ln K 1 + n ln s (8.26)
#
The problem statement provides us with two values of both P s and s; thus, we can solve for K 1
and n from two independent equations, and using values for these two parameters it is possible
#
to determine P s at a stress of 10 MPa.
Incorporating the two sets of data into Equation 8.26 leads to the following two independent
expressions:
-4
-1
ln(2.0 * 10 h ) = ln K 1 + (n)ln(3 MPa)
-1
ln(3.65 h ) = ln K 1 + (n)ln(25 MPa)