Page 28 - Mathematical Techniques of Fractional Order Systems

18 Mathematical Techniques of Fractional Order Systems

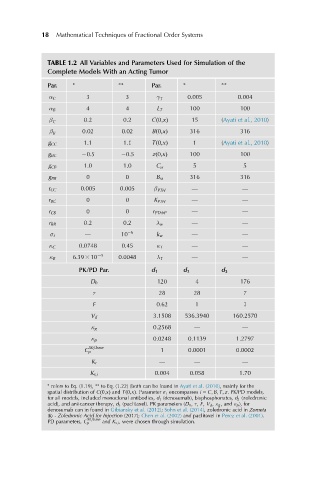
TABLE 1.2 All Variables and Parameters Used for Simulation of the
Complete Models With an Acting Tumor
Par. Par.
α C 3 3 γ T 0.005 0.004
α B 4 4 L T 100 100
0.2 0.2 15 (Ayati et al., 2010)
β C Cð0;xÞ
β B 0.02 0:02 Bð0;xÞ 316 316
g CC 1.1 1.1 Tð0;xÞ 1 (Ayati et al., 2010)
g BC 20:5 20:5 zð0;xÞ 100 100
g CB 1.0 1.0 C ss 5 5
g BB 0 0 B ss 316 316
r CC 0.005 0.005 β PTH — —
r BC 0 0 K PTH — —
r CB 0 0 r PTHrP — —
r BB 0.2 0.2 λ w — —
σ i — 10 26 k w — —
κ C 0.0748 0.45 κ T — —
κ B 6:39 3 10 24 0.0048 λ T — —
PK/PD Par. d 1 d 2 d 3

D 0 120 4 176
τ 28 28 7
F 0.62 1 1
V d 3.1508 536.3940 160.2570
κ g 0.2568 — —
κ p 0.0248 0.1139 1.2797
50=base
C p 1 0.0001 0.0002
K r — — —
K s;i 0.004 0.058 1.70
refers to Eq. (1.19), to Eq. (1.22) (both can be found in Ayati et al. (2010), mainly for the

spatial distribution of Cð0;xÞ and Tð0;xÞ. Parameter σ i encompasses i 5 C; B; T; z. PK/PD models,
for all models, included monoclonal antibodies, d 1 (denosumab), bisphosphonates, d 2 (zoledronic
acid), and anticancer therapy, d 3 (paclitaxel). PK parameters (D 0 , τ, F, V d , κ g , and κ p ), for
denosumab can in found in Gibiansky et al. (2012); Sohn et al. (2014), zoledronic acid in Zometa
s - Zoledronic Acid for Injection (2017); Chen et al. (2002) and paclitaxel in Perez et al. (2001).
50=base
PD parameters, C p and K s;i , were chosen through simulation.