Page 29 - Mathematical Techniques of Fractional Order Systems

Variable Order Fractional Derivatives and Bone Remodeling Chapter | 1 19

Healthy vs tumorous bone Healthy bone
Osteoclasts [cells] 20 Tumor disrupted bone
25
15
10
0 5
0 200 400 600 800 1000 1200
1000
Osteoblasts [cells] 800 Healthy bone
Tumor disrupted bone
600
400
200
0
0 200 400 600 800 1000 1200
120 Healthy bone
Bone mass [%] 80 Tumor disrupted bone
100
60
40
20
0
0 200 400 600 800 1000 1200
Time t [days]
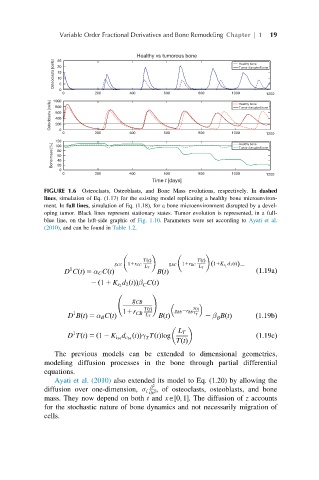
FIGURE 1.6 Osteoclasts, Osteoblasts, and Bone Mass evolutions, respectively. In dashed
lines, simulation of Eq. (1.17) for the existing model replicating a healthy bone microenviron-
ment. In full lines, simulation of Eq. (1.18), for a bone microenvironment disrupted by a devel-
oping tumor. Black lines represent stationary states. Tumor evolution is represented, in a full-
blue line, on the left-side graphic of Fig. 1.10. Parameters were set according to Ayati et al.
(2010), and can be found in Table 1.2.

TðtÞ TðtÞ
d
g CC 11r CC g BC 11r BC ð 11K s 1 1 ðtÞÞ
L T L T
1
D CðtÞ 5 α C CðtÞ BðtÞ ð1:19aÞ
d
2 ð1 1 K s 2 2 ðtÞÞβ CðtÞ
C
!
g CB

TðtÞ TðtÞ
1 g BB 2r BB L T
D BðtÞ 5 α B CðtÞ 11r CB L T BðtÞ 2 β BðtÞ ð1:19bÞ
B

1 L T
d ðtÞÞγ TðtÞlog
D TðtÞ 5 ð1 2 K i 34 c 34 T ð1:19cÞ
TðtÞ
The previous models can be extended to dimensional geometries,
modeling diffusion processes in the bone through partial differential
equations.
Ayati et al. (2010) also extended its model to Eq. (1.20) by allowing the
2
@
diffusion over one-dimension, σ i @x 2 , of osteoclasts, osteoblasts, and bone
mass. They now depend on both t and xA½0; 1Š. The diffusion of z accounts
for the stochastic nature of bone dynamics and not necessarily migration of
cells.