Page 347 - Mathematical Techniques of Fractional Order Systems

Multiswitching Synchronization Chapter | 11 337

απ
jargðλ i Þj . ð11:31Þ
2
if we choose
2 3
a 1 2 26 0 0 0
0 21 0 0
6 7
A 5 6 7 ð11:32Þ
0 0 a 4 2 5 0
4 5
0 0 0 21
Then the eigenvalues of the linear system (11.30) are 21, 21, 21, and
21. Hence the condition (11.31) is satisfied for and we get the required
synchronization. Numerical discussions for switch 2 are illustrated to verify
the theoretical results. The initial states of the master and slave system
are arbitrarily chosen as ðx 1 ð0Þ; y 1 ð0Þ; z 1 ð0Þ; w 1 ð0ÞÞ 5 ð4; 5; 6; 4Þ and
ðx 2 ð0Þ; y 2 ð0Þ; z 2 ð0Þ; w 2 ð0ÞÞ 5 ð2 2; 3; 2 1; 6Þ. The corresponding initial con-
dition for the error states is obtained as ðe 1 ð0Þ; e 2 ð0Þ; e 3 ð0Þ;
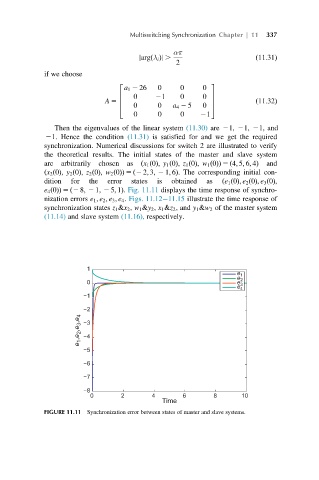
e 4 ð0ÞÞ 5 ð2 8; 2 1; 2 5; 1Þ. Fig. 11.11 displays the time response of synchro-
nization errors e 1 ; e 2 ; e 3 ; e 4 . Figs. 11.12 11.15 illustrate the time response of
synchronization states z 1 &x 2 , w 1 &y 2 , x 1 &z 2 , and y 1 &w 2 of the master system
(11.14) and slave system (11.16), respectively.

1
e 1
e 2
0 e 3
e 4
−1
−2
e 1 ,e 2 ,e 3 ,e 4 −3

−4

−5
−6
−7

−8
0 2 4 6 8 10
Time
FIGURE 11.11 Synchronization error between states of master and slave systems.