Page 343 - Mathematical Techniques of Fractional Order Systems

Multiswitching Synchronization Chapter | 11 333

4
e
e 1 2
e
3
2 e 4
0
e 1 ,e 2 ,e 3 ,e 4 −2

−4

−6

−8
0 2 4 6 8 10
Time
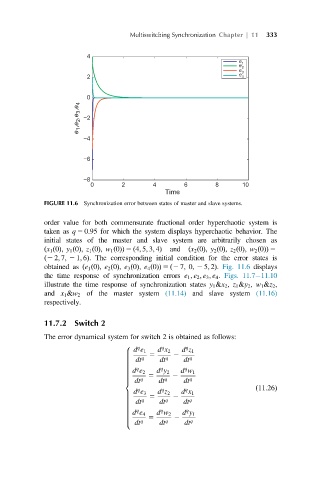
FIGURE 11.6 Synchronization error between states of master and slave systems.

order value for both commensurate fractional order hyperchaotic system is
taken as q 5 0:95 for which the system displays hyperchaotic behavior. The
initial states of the master and slave system are arbitrarily chosen as
ðx 1 ð0Þ; y 1 ð0Þ; z 1 ð0Þ; w 1 ð0ÞÞ 5 ð4; 5; 3; 4Þ and ðx 2 ð0Þ; y 2 ð0Þ; z 2 ð0Þ; w 2 ð0ÞÞ 5
ð2 2; 7; 2 1; 6Þ. The corresponding initial condition for the error states is
obtained as ðe 1 ð0Þ; e 2 ð0Þ; e 3 ð0Þ; e 4 ð0ÞÞ 5 ð2 7; 0; 2 5; 2Þ. Fig. 11.6 displays
the time response of synchronization errors e 1 ; e 2 ; e 3 ; e 4 . Figs. 11.7 11.10
illustrate the time response of synchronization states y 1 &x 2 , z 1 &y 2 , w 1 &z 2 ,
and x 1 &w 2 of the master system (11.14) and slave system (11.16)
respectively.

11.7.2 Switch 2
The error dynamical system for switch 2 is obtained as follows:

8 q q q
d e 1 d x 2 d z 1
> 5 2
>
> q q q
> dt dt dt
>
>
>
q q q
>
d e 2 d y 2 d w 1
>
>
> 5 2
dt dt dt
> q q q
>
<
q q q ð11:26Þ
d e 3 d z 2 d x 1
>
> 5 2
> q q q
> dt dt dt
>
>
>
> q q q
>
> d e 4 d w 2 d y 1
> 5 2
>
> q q q
: dt dt dt