Page 340 - Mathematical Techniques of Fractional Order Systems

330 Mathematical Techniques of Fractional Order Systems

(A) (B)
40 150

20 100
w 2 (t) 0 z 2 (t) 50

−20 0

−40 −50
−50 0 50 100 −100 −50 0 50
x (t) y 2 (t)
2
(C) (D)
40 40
20 20

w 2 (t) 0 w 2 (t) 0

−20 −20
−40 −40
−100 −50 0 50 −50 0 50 100 150
y 2 (t) (t)
z 2
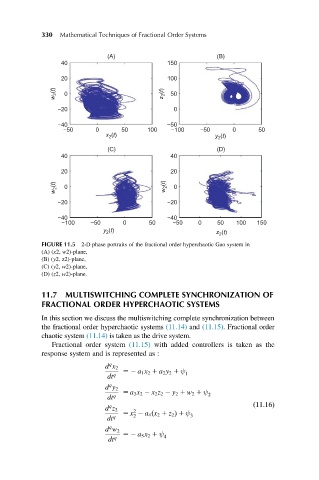
FIGURE 11.5 2-D phase portraits of the fractional order hyperchaotic Gao system in
(A) (x2, w2)-plane,
(B) (y2, z2)-plane,
(C) (y2, w2)-plane,
(D) (z2, w2)-plane.

11.7 MULTISWITCHING COMPLETE SYNCHRONIZATION OF
FRACTIONAL ORDER HYPERCHAOTIC SYSTEMS
In this section we discuss the multiswitching complete synchronization between
the fractional order hyperchaotic systems (11.14) and (11.15). Fractional order
chaotic system (11.14) is taken as the drive system.
Fractional order system (11.15) with added controllers is taken as the
response system and is represented as :
q
d x 2 52 a 1 x 2 1 a 2 y 2 1 ψ
dt q 1
q
d y 2 5 a 3 x 2 2 x 2 z 2 2 y 2 1 w 2 1 ψ
dt q 2
q ð11:16Þ
d z 2 5 x 2 a 4 ðx 2 1 z 2 Þ 1 ψ
2
dt q 2 3
q
d w 2
52 a 5 x 2 1 ψ
dt q 4