Page 339 - Mathematical Techniques of Fractional Order Systems

(A) (B)
10 30

5
20
w 1 (t) 0 z 1 (t)
10
−5

−10 0
−20 −10 0 10 20 −20 −10 0 10 20
x (t) y (t)
1
1
(C) (D)
10 10
5 5
w 1(t) 0 w 1 (t) 0

−5 −5

−10 −10
−20 −10 0 10 20 0 10 20 30
(t) z (t)
y 1 1
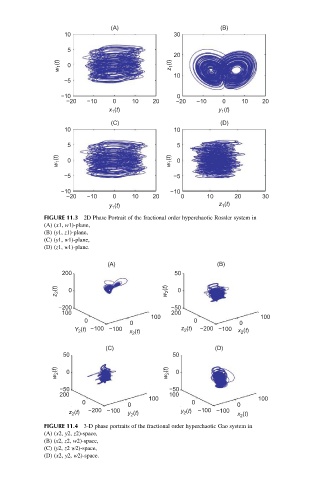
FIGURE 11.3 2D Phase Portrait of the fractional order hyperchaotic Rossler system in
(A) (x1, w1)-plane,
(B) (y1, z1)-plane,
(C) (y1, w1)-plane,
(D) (z1, w1)-plane.

(A) (B)
200 50
z 2 (t) 0 w 2 (t) 0

−200 −50
100 200
100 100
0 0
0 0
(t) −100 −100 z (t) −200 −100
Y 2 x (t) 2 x 2 (t)
2
(C) (D)
50 50
w 2 (t) 0 w 2 (t) 0

−50 −50
200 100
100 100
0 0 0 0 0 0 0 0
z (t) −200 −100 y (t) y 2 (t) −100 −100 x 2 (t)
2
2
FIGURE 11.4 3-D phase portraits of the fractional order hyperchaotic Gao system in
(A) (x2, y2, z2)-space,
(B) (x2, z2, w2)-space,
(C) (y2, z2 w2)-space,
(D) (x2, y2, w2)-space.