Page 448 - Mathematical Techniques of Fractional Order Systems
P. 448
Applications of Continuous-time Fractional Order Chapter | 14 433
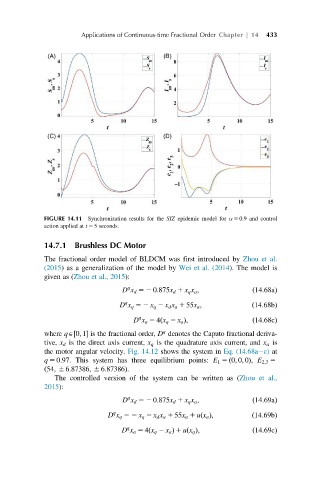
FIGURE 14.11 Synchronization results for the SIZ epidemic model for α 5 0:9 and control
action applied at t 5 5 seconds.
14.7.1 Brushless DC Motor
The fractional order model of BLDCM was first introduced by Zhou et al.
(2015) as a generalization of the model by Wei et al. (2014). The model is
given as (Zhou et al., 2015):
q
D x d 52 0:875x d 1 x q x a ; ð14:68aÞ
q
D x q 52 x q 2 x d x a 1 55x a ; ð14:68bÞ
q
D x a 5 4ðx q 2 x a Þ; ð14:68cÞ
q
where qA½0; 1 is the fractional order, D denotes the Caputo fractional deriva-
tive, x d is the direct axis current, x q is the quadrature axis current, and x a is
the motor angular velocity. Fig. 14.12 shows the system in Eq. (14.68a c) at
q 5 0:97. This system has three equilibrium points: E 1 5 ð0; 0; 0Þ, E 2;3 5
ð54; 6 6:87386; 6 6:87386Þ.
The controlled version of the system can be written as (Zhou et al.,
2015):
q
D x d 52 0:875x d 1 x q x a ; ð14:69aÞ
q
D x q 52 x q 2 x d x a 1 55x a 1 uðx a Þ; ð14:69bÞ
q
D x a 5 4ðx q 2 x a Þ 1 uðx q Þ; ð14:69cÞ