Page 497 - Mathematical Techniques of Fractional Order Systems

484 Mathematical Techniques of Fractional Order Systems

1.1
1

0.9
0.8
x
0.7
0.6

0.5
0.4
0.05 0.1 0.15 0.2 0.25
a
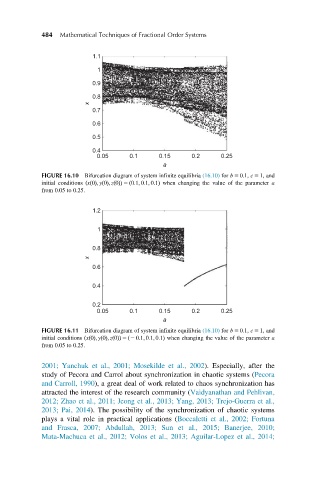
FIGURE 16.10 Bifurcation diagram of system infinite equilibria (16.10) for b 5 0:1, c 5 1, and
initial conditions ðxð0Þ; yð0Þ; zð0ÞÞ 5 ð0:1; 0:1; 0:1Þ when changing the value of the parameter a
from 0.05 to 0.25.

1.2

1

0.8
x
0.6

0.4

0.2
0.05 0.1 0.15 0.2 0.25
a
FIGURE 16.11 Bifurcation diagram of system infinite equilibria (16.10) for b 5 0:1, c 5 1, and
initial conditions ðxð0Þ; yð0Þ; zð0ÞÞ 5 ð2 0:1; 0:1; 0:1Þ when changing the value of the parameter a
from 0.05 to 0.25.

2001; Yanchuk et al., 2001; Mosekilde et al., 2002). Especially, after the
study of Pecora and Carrol about synchronization in chaotic systems (Pecora
and Carroll, 1990), a great deal of work related to chaos synchronization has
attracted the interest of the research community (Vaidyanathan and Pehlivan,
2012; Zhao et al., 2011; Jeong et al., 2013; Yang, 2013; Trejo-Guerra et al.,
2013; Pai, 2014). The possibility of the synchronization of chaotic systems
plays a vital role in practical applications (Boccaletti et al., 2002; Fortuna
and Frasca, 2007; Abdullah, 2013; Sun et al., 2015; Banerjee, 2010;
Mata-Machuca et al., 2012; Volos et al., 2013; Aguilar-Lopez et al., 2014;