Page 502 - Mathematical Techniques of Fractional Order Systems

Dynamics, Synchronization and Fractional Order Form Chapter | 16 489

(A) (B)
1.5 1.5
1 1
0.5 0.5
x 1 , x 2 0 y 1 , y 2 0
−0.5 −0.5

−1 −1
−1.5 −1.5
900 920 940 960 980 1000 900 920 940 960 980 1000
Time Time
(C)
1.5
1
0.5
z 1 , z 2 0

−0.5
−1
−1.5
900 920 940 960 980 1000
Time
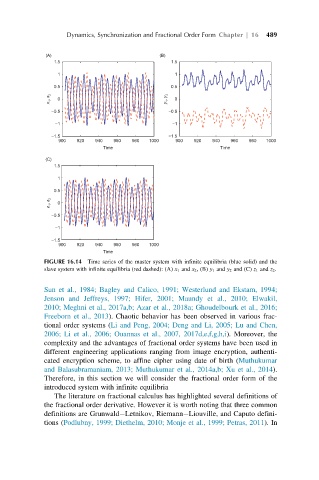
FIGURE 16.14 Time series of the master system with infinite equilibria (blue solid) and the
slave system with infinite equilibria (red dashed): (A) x 1 and x 2 , (B) y 1 and y 2 and (C) z 1 and z 2 .

Sun et al., 1984; Bagley and Calico, 1991; Westerlund and Ekstam, 1994;
Jenson and Jeffreys, 1997; Hifer, 2001; Maundy et al., 2010; Elwakil,
2010; Meghni et al., 2017a,b; Azar et al., 2018a; Ghoudelbourk et al., 2016;
Freeborn et al., 2013). Chaotic behavior has been observed in various frac-
tional order systems (Li and Peng, 2004; Deng and Li, 2005; Lu and Chen,
2006; Li et al., 2006; Ouannas et al., 2007, 2017d,e,f,g,h,i). Moreover, the
complexity and the advantages of fractional order systems have been used in
different engineering applications ranging from image encryption, authenti-
cated encryption scheme, to affine cipher using date of birth (Muthukumar
and Balasubramaniam, 2013; Muthukumar et al., 2014a,b; Xu et al., 2014).
Therefore, in this section we will consider the fractional order form of the
introduced system with infinite equilibria
The literature on fractional calculus has highlighted several definitions of
the fractional order derivative. However it is worth noting that three common
definitions are Grunwald Letnikov, Riemann Liouville, and Caputo defini-
tions (Podlubny, 1999; Diethelm, 2010; Monje et al., 1999; Petras, 2011). In