Page 506 - Mathematical Techniques of Fractional Order Systems

Dynamics, Synchronization and Fractional Order Form Chapter | 16 493

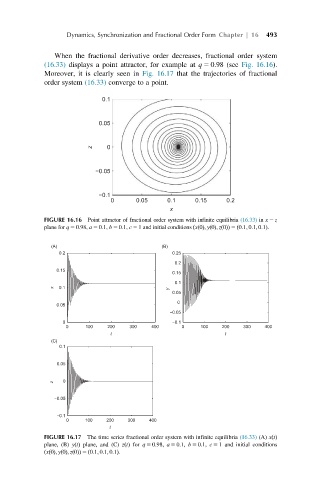
When the fractional derivative order decreases, fractional order system
(16.33) displays a point attractor, for example at q 5 0:98 (see Fig. 16.16).
Moreover, it is clearly seen in Fig. 16.17 that the trajectories of fractional
order system (16.33) converge to a point.

0.1

0.05

z 0

−0.05

−0.1
0 0.05 0.1 0.15 0.2
x
FIGURE 16.16 Point attractor of fractional order system with infinite equilibria (16.33) in x 2 z
plane for q 5 0:98, a 5 0:1, b 5 0:1, c 5 1 and initial conditions ðxð0Þ; yð0Þ; zð0ÞÞ 5 ð0:1; 0:1; 0:1Þ.

(A) (B)
0.2 0.25
0.2
0.15
0.15
0.1
x 0.1 y
0.05
0
0.05
−0.05
0 −0.1
0 100 200 300 400 0 100 200 300 400
t t
(C)
0.1

0.05

0
z
−0.05

−0.1
0 100 200 300 400
t
FIGURE 16.17 The time series fractional order system with infinite equilibria (16.33) (A) xðtÞ
plane, (B) yðtÞ plane, and (C) zðtÞ for q 5 0:98, a 5 0:1, b 5 0:1, c 5 1 and initial conditions
ðxð0Þ; yð0Þ; zð0ÞÞ 5 ð0:1; 0:1; 0:1Þ.