Page 584 - Mathematical Techniques of Fractional Order Systems

554 Mathematical Techniques of Fractional Order Systems

(A) Chebyshev (B) Circle
CGWO CGWO
CGOA
CGOA
Mean convergence curve 10 0 −2 GOA Mean convergence curve 10 0 −2 GOA
GWO
GWO
10
10

100 200 300 400 100 200 300 400
Iteration number Iteration number
(C) Gauss mouse (D) Iterative
CGWO CGWO
CGOA 0 CGOA
Mean convergence curve 10 −2 Mean convergence curve 10 −2
GWO
GWO
0
GOA
10
GOA
10
100 200 300 400 100 200 300 400
Iteration number Iteration number
(E) Logistic (F) Piecewise
CGWO CGWO
CGOA
CGOA
Mean convergence curve 10 0 −2 GOA Mean convergence curve 10 0 −2 GOA
GWO
GWO
10
10

100 200 300 400 100 200 300 400
Iteration number Iteration number
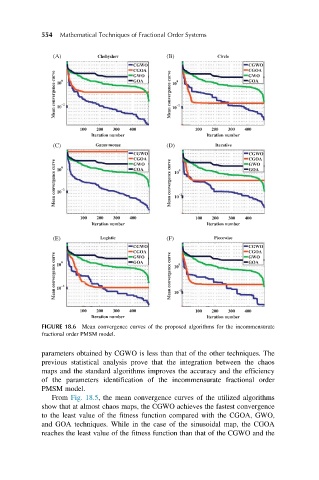
FIGURE 18.6 Mean convergence curves of the proposed algorithms for the incommensurate
fractional order PMSM model.

parameters obtained by CGWO is less than that of the other techniques. The
previous statistical analysis prove that the integration between the chaos
maps and the standard algorithms improves the accuracy and the efficiency
of the parameters identification of the incommensurate fractional order
PMSM model.
From Fig. 18.5, the mean convergence curves of the utilized algorithms
show that at almost chaos maps, the CGWO achieves the fastest convergence
to the least value of the fitness function compared with the CGOA, GWO,
and GOA techniques. While in the case of the sinusoidal map, the CGOA
reaches the least value of the fitness function than that of the CGWO and the