Page 674 - Mathematical Techniques of Fractional Order Systems

Fractional Order Chaotic Systems Chapter | 21 645

relation (21.15), according to Grigorenko and Grigorenko (2003) this system
can be chaotic only when the following condition is satisfied p . 0.993.
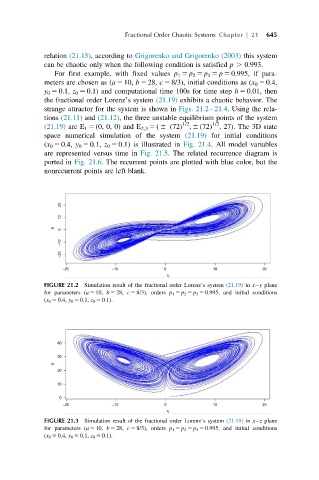
For first example, with fixed values p 1 5 p 2 5 p 3 5 p 5 0.995, if para-
meters are chosen as (a 5 10, b 5 28, c 5 8/3), initial conditions as (x 0 5 0.4,
y 0 5 0.1, z 0 5 0.1) and computational time 100s for time step h 5 0.01, then
the fractional order Lorenz’s system (21.19) exhibits a chaotic behavior. The
strange attractor for the system is shown in Figs. 21.2 21.4. Using the rela-
tions (21.11) and (21.12), the three unstable equilibrium points of the system
1/2
1/2
(21.19) are E 1 5 (0, 0, 0) and E 2,3 5 ( 6 (72) , 6 (72) , 27). The 3D state
space numerical simulation of the system (21.19) for initial conditions
(x 0 5 0.4, y 0 5 0.1, z 0 5 0.1) is illustrated in Fig. 21.4. All model variables
are represented versus time in Fig. 21.5. The related recurrence diagram is
ported in Fig. 21.6. The recurrent points are plotted with blue color, but the
nonrecurrent points are left blank.

FIGURE 21.2 Simulation result of the fractional order Lorenz’s system (21.19) in x y plane
for parameters (a 5 10, b 5 28, c 5 8/3), orders p 1 5 p 2 5 p 3 5 0.995, and initial conditions
(x 0 5 0.4, y 0 5 0.1, z 0 5 0.1).

FIGURE 21.3 Simulation result of the fractional order Lorenz’s system (21.19) in x z plane
for parameters (a 5 10, b 5 28, c 5 8/3), orders p 1 5 p 2 5 p 3 5 0.995, and initial conditions
(x 0 5 0.4, y 0 5 0.1, z 0 5 0.1).