Page 675 - Mathematical Techniques of Fractional Order Systems

646 Mathematical Techniques of Fractional Order Systems

50
40
30
z t 30 y t
20 20
10
10 0
–10
0 –30 –20
–20 –10 0 10 20
x
t
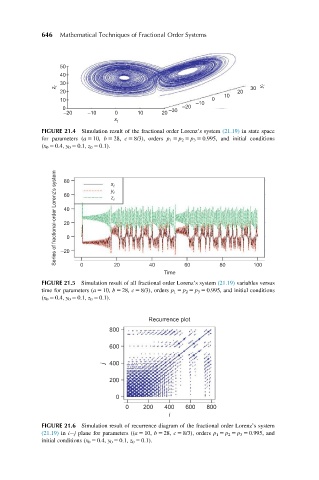
FIGURE 21.4 Simulation result of the fractional order Lorenz’s system (21.19) in state space
for parameters (a 5 10, b 5 28, c 5 8/3), orders p 1 5 p 2 5 p 3 5 0.995, and initial conditions
(x 0 5 0.4, y 0 5 0.1, z 0 5 0.1).

Series of fractional-order Lorenz’s system 60 0 x t t t
80
y
z
40
20

–20
20
40
0
Time 60 80 100
FIGURE 21.5 Simulation result of all fractional order Lorenz’s system (21.19) variables versus
time for parameters (a 5 10, b 5 28, c 5 8/3), orders p 1 5 p 2 5 p 3 5 0.995, and initial conditions
(x 0 5 0.4, y 0 5 0.1, z 0 5 0.1).

Recurrence plot
800

600

400
j
200

0
0 200 400 600 800
i
FIGURE 21.6 Simulation result of recurrence diagram of the fractional order Lorenz’s system
(21.19) in i j plane for parameters ((a 5 10, b 5 28, c 5 8/3), orders p 1 5 p 2 5 p 3 5 0.995, and
initial conditions (x 0 5 0.4, y 0 5 0.1, z 0 5 0.1).