Page 678 - Mathematical Techniques of Fractional Order Systems

Fractional Order Chaotic Systems Chapter | 21 649

Step 6: Execute the iterative algorithm for topological synchronization on
master slave system with while tracking control for chaotic nonlinear frac-
tional order systems.
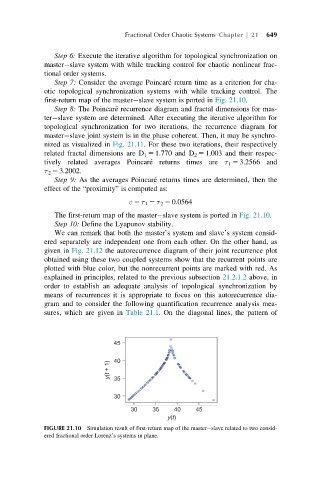
Step 7: Consider the average Poincare ´ return time as a criterion for cha-
otic topological synchronization systems with while tracking control. The
first-return map of the master slave system is ported in Fig. 21.10.
Step 8: The Poincare ´ recurrence diagram and fractal dimensions for mas-
ter slave system are determined. After executing the iterative algorithm for
topological synchronization for two iterations, the recurrence diagram for
master slave joint system is in the phase coherent. Then, it may be synchro-
nized as visualized in Fig. 21.11. For these two iterations, their respectively
related fractal dimensions are D 1 5 1.770 and D 2 5 1.003 and their respec-
tively related averages Poincare ´ returns times are τ 1 5 3.2566 and
τ 2 5 3.2002.
Step 9: As the averages Poincare ´ returns times are determined, then the
effect of the “proximity” is computed as:

ε 5 τ 1 2 τ 2 5 0:0564
The first-return map of the master slave system is ported in Fig. 21.10.
Step 10: Define the Lyapunov stability.
We can remark that both the master’s system and slave’s system consid-
ered separately are independent one from each other. On the other hand, as
given in Fig. 21.12 the autorecurrence diagram of their joint recurrence plot
obtained using these two coupled systems show that the recurrent points are
plotted with blue color, but the nonrecurrent points are marked with red. As
explained in principles, related to the previous subsection 21.2.1.2 above, in
order to establish an adequate analysis of topological synchronization by
means of recurrences it is appropriate to focus on this autorecurrence dia-
gram and to consider the following quantification recurrence analysis mea-
sures, which are given in Table 21.1. On the diagonal lines, the pattern of

45

y(t + 1) 40

35
30

30 35 40 45
y(t)
FIGURE 21.10 Simulation result of first-return map of the master slave related to two consid-
ered fractional order Lorenz’s systems in plane.