Page 677 - Mathematical Techniques of Fractional Order Systems

648 Mathematical Techniques of Fractional Order Systems

Recurrence plot
800

600
400
j
200

0
0 200 400 600 800
i
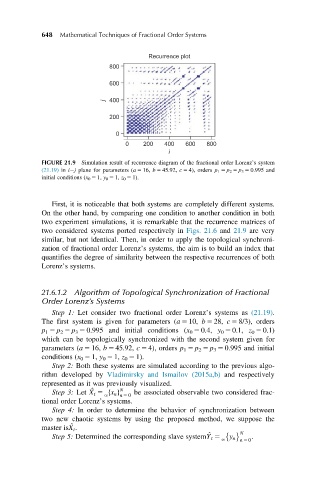
FIGURE 21.9 Simulation result of recurrence diagram of the fractional order Lorenz’s system
(21.19) in i j plane for parameters (a 5 16, b 5 45.92, c 5 4), orders p 1 5 p 2 5 p 3 5 0.995 and
initial conditions (x 0 5 1, y 0 5 1, z 0 5 1).

First, it is noticeable that both systems are completely different systems.
On the other hand, by comparing one condition to another condition in both
two experiment simulations, it is remarkable that the recurrence matrices of
two considered systems ported respectively in Figs. 21.6 and 21.9 are very
similar, but not identical. Then, in order to apply the topological synchroni-
zation of fractional order Lorenz’s systems, the aim is to build an index that
quantifies the degree of similarity between the respective recurrences of both
Lorenz’s systems.

21.6.1.2 Algorithm of Topological Synchronization of Fractional
Order Lorenz’s Systems
Step 1: Let consider two fractional order Lorenz’s systems as (21.19).
The first system is given for parameters (a 5 10, b 5 28, c 5 8/3), orders
p 1 5 p 2 5 p 3 5 0.995 and initial conditions (x 0 5 0.4, y 0 5 0.1, z 0 5 0.1)
which can be topologically synchronized with the second system given for
parameters (a 5 16, b 5 45.92, c 5 4), orders p 1 5 p 2 5 p 3 5 0.995 and initial
conditions (x 0 5 1, y 0 5 1, z 0 5 1).
Step 2: Both these systems are simulated according to the previous algo-
rithm developed by Vladimirsky and Ismailov (2015a,b) and respectively
represented as it was previously visualized.
^ N
Step 3: Let X t 5 fg be associated observable two considered frac-
α
x n n 5 0
tional order Lorenz’s systems.
Step 4: In order to determine the behavior of synchronization between
two new chaotic systems by using the proposed method, we suppose the
^
master isX t .
^
Step 5: Determined the corresponding slave systemY t 5 α N .
y n
n 5 0