Page 337 - Matrix Analysis & Applied Linear Algebra

5.6 Unitary and Orthogonal Matrices 333

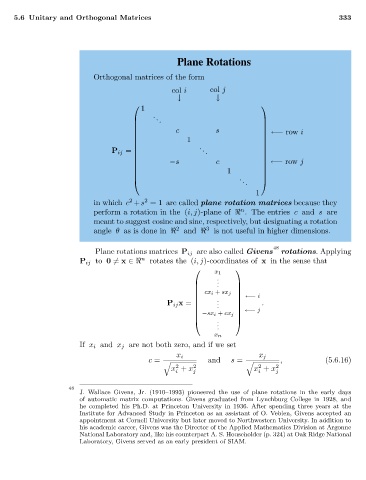
Plane Rotations

Orthogonal matrices of the form
col i col j
↓ ↓
1
 
.
 . . 
 
c s  ←− row i
 

1
 
 
 . . 
P ij =  . 
 
−s c  ←− row j

 
 1 
.
 
 . . 
1
2
2
in which c +s =1 are called plane rotation matrices because they
n
perform a rotation in the (i, j)-plane of . The entries c and s are
meant to suggest cosine and sine, respectively, but designating a rotation
2
3
angle θ as is done in and is not useful in higher dimensions.
48
Plane rotations matrices P ij are also called Givens rotations. Applying
n
P ij to 0 = x ∈ rotates the (i, j)-coordinates of x in the sense that
 
x 1
.
 . . 
 
 cx i + sx j 
 .  ←− i
P ij x =  .  .
 . 
  ←− j
 −sx i + cx j 
.
 
.
.
x n
If x i and x j are not both zero, and if we set
x i x j
and , (5.6.16)
c = s =
2
2
x + x 2 x + x 2
i j i j
48
J. Wallace Givens, Jr. (1910–1993) pioneered the use of plane rotations in the early days
of automatic matrix computations. Givens graduated from Lynchburg College in 1928, and
he completed his Ph.D. at Princeton University in 1936. After spending three years at the
Institute for Advanced Study in Princeton as an assistant of O. Veblen, Givens accepted an
appointment at Cornell University but later moved to Northwestern University. In addition to
his academic career, Givens was the Director of the Applied Mathematics Division at Argonne
National Laboratory and, like his counterpart A. S. Householder (p. 324) at Oak Ridge National
Laboratory, Givens served as an early president of SIAM.