Page 40 - Mechanical Engineers Reference Book

Mechanics of fluids 1/29

where v is the velocity within the boundary layer at a distance
y above the plate surface. (The integral

may be defined as the momentum thickness (e) and the
integral
1' (1 - 3.

as the displacement thickness (6") so that
FD = p4e.) (1.76)

In order to solve the Von Karman integral equation (1.75)
or equation (1.76) it is necessary to know the value of 6 and
the relationship between v and y. the velocity distribution.
Both of these are dependent on each other and the flow
Fast ' ' j Slow flow regime, laminar or turbulent, within the boundary layer.
I
-1- 1 S.6.1 Laminar boundary layers
1
-- !
flow
DF Dc DS Depth, D A laminar boundary is normally assumed if Re, < 500 000.
(Re, is Reynolds' number based on x or pvsyIq.) For laminar
boundary layers various simplified velocity distribution rela-
Figure 1.43 Graph of specific energy versus channel depth
tionships may be used, such as linear, sinusoidal or cosinsu-
soidal. The generally accepted most accurate relationship is,
however, that obtained by the reduction of a four-term
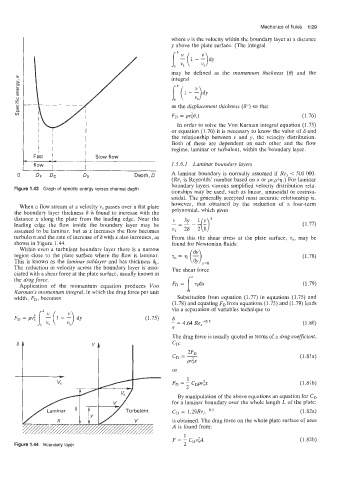
When a flow stream at a velocity v, passes over a flat plate
the boundary layer thickness 6 is found to increase with the polynomial, which gives
distance x along the plate from the leading edge. Near the
leading edge the flow inside the boundary layer may be (1.77)
assumed to be laminar, but as x increases the flow becomes
turbulent and the rate of increase of 6 with x also increases, as From this the shear stress at the plate surface, T~, may be
shown in Figure 1.44. found for Newtonian fluids:
Within even a turbulent boundary layer there is a narrow
region close to the plate surface where the flow is laminar. (1.78)
This is known as the laminar sublayer and has thickness St,.
The redluction in velocity across the boundary layer is asso- The shear force
ciated with a shear force at the plate surface, usually known as FD = ix
the drag force.
Application of the momentum equation produces Von TOdw (1.79)
KarmanS momentum integral, in which the drag force per unit
width, FD, becomes Substitution from equation (1.77) in equations (1.75) and
(1.78) and equating FD,from equations (1.75) and (1.79) leads
via a separation of variables technique to
(1.75) 6
- = 4.64 (1.80)
X
The drag force is usually quoted in terms of a drag coefficient,
CD :
(1.81a)
- or
I I A- (1.81b)

By manipulation of the above equations an equation for CD
for a laminar boundary over the whole length L of the plate:
OI f. C, = 1.29ReL-05 (1 32a)

X is obtained. The drag force on the whole plate surface of area
A is found from:
1
F = - cD~A (1.82b)
Figure 1.44 Boundary layer 2