Page 477 - Mechanical Engineers' Handbook (Volume 2)

468 Closed-Loop Control System Analysis

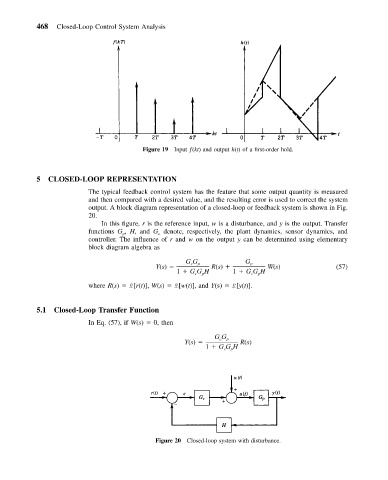
Figure 19 Input ƒ(kt) and output h(t) of a first-order hold.

5 CLOSED-LOOP REPRESENTATION
The typical feedback control system has the feature that some output quantity is measured
and then compared with a desired value, and the resulting error is used to correct the system
output. A block diagram representation of a closed-loop or feedback system is shown in Fig.
20.
In this figure, r is the reference input, w is a disturbance, and y is the output. Transfer
functions G , H, and G denote, respectively, the plant dynamics, sensor dynamics, and
p
c
controller. The influence of r and w on the output y can be determined using elementary
block diagram algebra as
GG p G p
c
Y(s) R(s) W(s) (57)
1 GG H 1 GG H
c p c p
where R(s) L[r(t)], W(s) L[w(t)], and Y(s) L[y(t)].

5.1 Closed-Loop Transfer Function

In Eq. (57), if W(s) 0, then
GG
Y(s) c p R(s)
1 GG H
p
c

Figure 20 Closed-loop system with disturbance.