Page 817 - Mechanical Engineers' Handbook (Volume 2)

808 Neural Networks in Feedback Control Systems

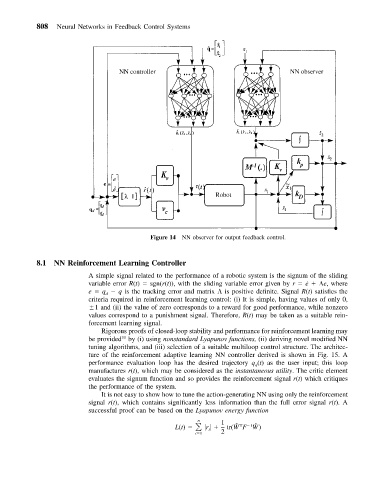
Figure 14 NN observer for output feedback control.

8.1 NN Reinforcement Learning Controller
A simple signal related to the performance of a robotic system is the signum of the sliding
variable error R(t) sgn(r(t)), with the sliding variable error given by r ˙e e, where
e q q is the tracking error and matrix is positive definite. Signal R(t) satisfies the
d
criteria required in reinforcement learning control: (i) It is simple, having values of only 0,
1 and (ii) the value of zero corresponds to a reward for good performance, while nonzero
values correspond to a punishment signal. Therefore, R(t) may be taken as a suitable rein-
forcement learning signal.
Rigorous proofs of closed-loop stability and performance for reinforcement learning may
31
be provided by (i) using nonstandard Lyapunov functions, (ii) deriving novel modified NN
tuning algorithms, and (iii) selection of a suitable multiloop control structure. The architec-
ture of the reinforcement adaptive learning NN controller derived is shown in Fig. 15. A
performance evaluation loop has the desired trajectory q (t) as the user input; this loop
d
manufactures r(t), which may be considered as the instantaneous utility. The critic element
evaluates the signum function and so provides the reinforcement signal r(t) which critiques
the performance of the system.
It is not easy to show how to tune the action-generating NN using only the reinforcement
signal r(t), which contains significantly less information than the full error signal r(t). A
successful proof can be based on the Lyapunov energy function
L(t) r 1 tr(WF W)
n
1 ˜
˜
T
i 1 i 2