Page 122 - Singiresu S. Rao-Mechanical Vibrations in SI Units, Global Edition-Pearson (2017)

problems 119
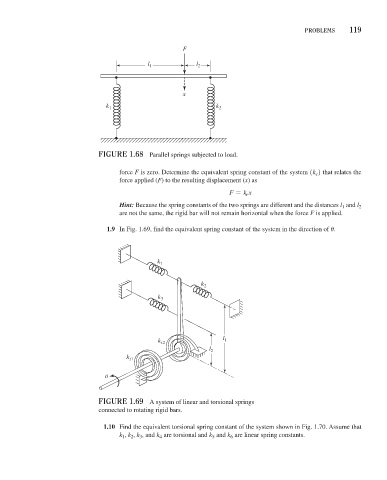
F

l 1 l 2

x
k 1 k 2

FiGure 1.68 Parallel springs subjected to load.

force F is zero. Determine the equivalent spring constant of the system 1k e 2 that relates the
force applied (F) to the resulting displacement (x) as
F = k e x

Hint: Because the spring constants of the two springs are different and the distances l 1 and l 2
are not the same, the rigid bar will not remain horizontal when the force F is applied.

1.9 In Fig. 1.69, find the equivalent spring constant of the system in the direction of u.

k 1

k 2
k 3

k t2 l 1
l 2
k t1

u

FiGure 1.69 A system of linear and torsional springs
connected to rotating rigid bars.

1.10 Find the equivalent torsional spring constant of the system shown in Fig. 1.70. Assume that
k 1 , k 2 , k 3 , and k 4 are torsional and k 5 and k 6 are linear spring constants.