Page 130 - Mechanics Analysis Composite Materials

Chapter 3. Mechanics of a unidirectional ply 115

Obviously

Then, Eq. (3.125) can be written in the form

(3.126)
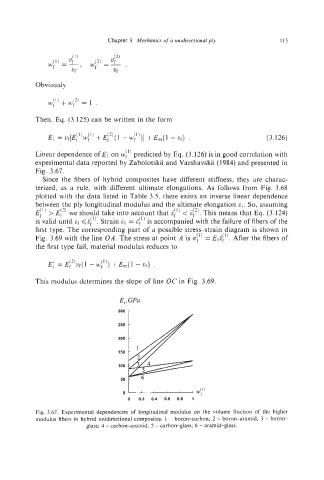
Linear dependence of El on w;” predicted by Eq. (3.126) is in good correlation with
experimental data reported by Zabolotskii and Varshavskii (1 984) and presented in
Fig. 3.67.
Since the fibers of hybrid composites have different stiffness, they are charac-
terized, as a rule, with different ultimate elongations. As follows from Fig. 3.68
plotted with the data listed in Table 3.5, there exists an inverse linear dependence
between the ply longitudinal modulus and the ultimate elongation El. So, assuming
E:,” > E!’) we should take into account that Ell) < This means that Eq. (3.124)
is valid until EI <E$’’. Strain E’ = El’) is accompanied with the failure of fibers of the
first type. The corresponding part of a possible stress-strain diagram is shown in
Fig. 3.69 with the line OA. The stress at point A is 01’) = EIE~’).After the fibers of
the first type fail, material modulus reduces to

This modulus determines the slope of line OC in Fig. 3.69.

E,,GPa
300 r

0
0 0.2 0.4 0.6 0.8 1
Fig. 3.67. Experimental dependencies of longitudinal modulus on the volume fraction of the higher
modulus fibers in hybrid unidirectional composites: I - boron*arbon; 2 - boron-aramid; 3 - boron-
glass; 4 - carbon-aramid; 5 - carbon-glass; 6 - aramid-glass.