Page 359 - Mechanics Analysis Composite Materials

344 Mechanics and analysis of composite materials

For laminates, such as in Fig. 7.34, the boundary conditions, Eqs. (7.59) should
be supplemented with the interlaminar conditions uf) = and cy)= cry-’).
Omitting rather cumbersome solution that can be found elsewhere (Vasiliev and
Sibiryakov, 1985) present some numerical results.
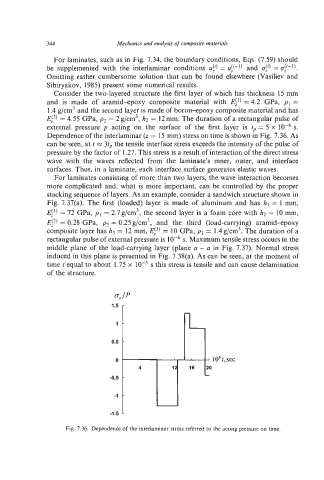
Consider the two-layered structure the first layer of which has thickness 15 mm
and is made of aramid-epoxy composite material with El’) = 4.2 GPa, pI =
1.4 g/cm3and the second layer is made of boron-epoxy composite material and has
E!2) = 4.55 GPa, p2 = 2g/cm3, h2 = 12mm. The duration of a rectangular pulse of
external pressure p acting on the surface of the first layer is tp = 5 x s.
Dependenceof the interlaminar (z = 15 mm) stress on time is shown in Fig. 7.36. As
can be seen, at t M 3tp the tensile interface stress exceeds the intensity of the pulse of
pressure by the factor of 1.27. This stress is a result of interaction of the direct stress
wave with the waves reflected from the laminate’s inner, outer, and interface
surfaces. Thus, in a laminate, each interface surface generates elastic waves.
For laminates consisting of more than two layers, the wave interaction becomes
more complicated and, what is more important, can be controlled by the proper
stacking sequence of layers. As an example, consider a sandwich structure shown in
Fig. 7.37(a). The first (loaded) layer is made of aluminum and has hl = 1 mm,
E!’) = 72 GPa, pI = 2.7g/cm3, the second layer is a foam core with h2 = 10 mm,
E!*) = 0.28 GPa, pz = 0.25 g/cm3, and the third (load-carrying) aramid+poxy
composite layer has h3 = 12 mm, Ei3)= 10 GPa, p3 = l.4g/cm3. The duration of a
rectangular pulse of external pressure is s. Maximum tensile stress occurs in the
middle plane of the load-carrying layer (plane a - a in Fig. 7.37). Normal stress
induced in this plane is presented in Fig. 7.38(a). As can be seen, at the moment of
time t equal to about 1.75 x low5s this stress is tensile and can cause delamination
of the structure.

-
1.5

1

0.5

0
4
-03

-I

-1.5 -